部分積分とは $\displaystyle\int x\cos xdx$ や $\displaystyle\int x^2e^{3x}dx$ のように「2つの関数のかけ算の形」を積分するための以下のような公式です:
$\displaystyle\int f(x)g(x) dx =f(x)g^*(x)-\displaystyle\int f(x)’g^*(x)dx$
部分積分の公式は、見た目は難しそうですが、慣れてしまえばそこまで難しくありません。このページでは、部分積分の基本から、部分積分を使うコツ、いろいろな例題など、部分積分について徹底的に解説します。
部分積分とは
部分積分は、2つの関数 $f(x)$、$g(x)$ のかけ算の積分 $\displaystyle\int f(x)g(x)dx$ を計算するときに使う以下のような公式です:
$\displaystyle\int f(x)g(x) dx =f(x)g^*(x)-\displaystyle\int f(x)’g^*(x)dx$
ただし、$f’$ は $f$ の微分、$g^*$ は $g$ の積分です。
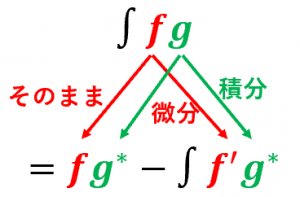
部分積分の公式の意味:
・$f$ と $g$ のかけ算の積分を
・$g$ だけ先に積分して
・$f$ は微分して簡単な形にする
ことによって積分するような公式です。
部分積分を使う簡単な例題
$\displaystyle\int x\cos xdx$
を計算してみましょう。
$f(x)=x$ と $g(x)=\cos x$ という2つの関数のかけ算の積分です。このような「かけ算の積分」には部分積分が有効な場合が多いです。
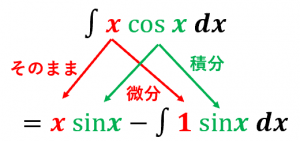
部分積分の公式を使うと、
$\displaystyle\int x\cos xdx\\
=x\sin x-\displaystyle\int 1\cdot\sin xdx\\
=x\sin x-(-\cos x)+C\\
=x\sin x+\cos x+C$
となります。
関連:xcosxの微分、グラフ、積分など
部分積分のコツ
部分積分では、$f$ と $g$ の積を積分します。$f$ と $g$ を選ぶ際に、
・$f$ は微分して簡単になる関数($x$、$x^2$、$\log x$ など)
・$g$ は積分しても難しくならない関数($\sin x$、$\cos x$、$e^x$ など)
を選ぶのがコツです。

例えば、先ほどの例 $\displaystyle\int x\cos xdx$ では
・$f$ は微分して簡単になる関数 $x$
・$g$ は積分しても難しくならない関数 $\cos x$
のように選ぶことができたので、部分積分が成功しています。
指数関数を含む例題
$\displaystyle\int xe^xdx$
を計算してみましょう。
・$f$ は微分して簡単になる関数 $x$
・$g$ は積分しても難しくならない関数 $e^x$
として部分積分を使うと、
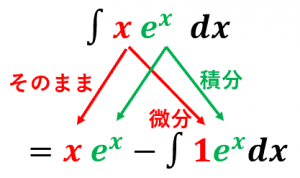
$\displaystyle\int xe^xdx\\
=xe^x-\displaystyle\int 1\cdot e^xdx\\
=xe^x-e^x+C$
となります。
関連:y=xe^xの微分、積分、グラフなど
関連:xe^{-x}の不定積分と広義積分
部分積分の公式の覚え方

$\displaystyle\int f(x)g(x) dx =f(x)g^*(x)-\displaystyle\int f(x)’g^*(x)dx$
という公式は、
「そのまま積分ー$\int$微分積分」
と覚えると覚えやすいです。
部分積分の応用1
$\displaystyle\int \log xdx$
を計算してみましょう。
部分積分は「2つの関数のかけ算」の形でないと使えません。そこで、$\log x=(\log x)\cdot 1$ なので、
$f(x)=\log x$、$g(x)=1$ とみなして部分積分を使います。
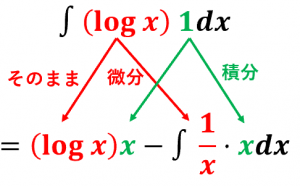
$\displaystyle\int\log xdx\\
=\displaystyle\int(\log x)\cdot 1dx\\
=(\log x)\cdot x-\displaystyle\int \dfrac{1}{x}\cdot xdx\\
=x\log x-x+C$
関連:logx、xlogx、logx/x、1/xlogxの積分
部分積分の応用2
$\displaystyle\int x^2e^{3x}dx$
を計算してみましょう。
$f(x)=x^2$ と $g(x)=e^{3x}$ のかけ算の積分なので、部分積分を使うと、
$\displaystyle\int x^2e^{3x}dx\\
=x^2\left(\dfrac{1}{3}e^{3x}\right)-\displaystyle\int(2x)\left(\dfrac{1}{3}e^{3x}\right)dx\\
=\dfrac{x^2e^{3x}}{3}-\dfrac{2}{3}\displaystyle\int xe^{3x}dx$
となります。第二項の積分は、$f(x)=x$ と $g(x)=e^{3x}$ のかけ算の積分なので、もう一度部分積分を使うと、
$\displaystyle\int xe^{3x}dx\\
=x\left(\dfrac{1}{3}e^{3x}\right)-\displaystyle\int 1\cdot\left(\dfrac{1}{3}e^{3x}\right)dx\\
=\dfrac{xe^{3x}}{3}-\dfrac{e^{3x}}{9}+C$
となります。
結局、
$\displaystyle\int x^2e^{3x}dx\\
=\dfrac{x^2e^{3x}}{3}-\dfrac{2}{9}xe^{3x}+\dfrac{2}{27}e^{3x}+C$
となります。
部分積分の公式の証明
部分積分の公式:
$\displaystyle\int f(x)g(x) dx =f(x)g^*(x)-\displaystyle\int f(x)’g^*(x)dx$
を証明してみます。
まず、積の微分公式より、
$(f(x)g^*(x))’=f(x)g(x)+f'(x)g^*(x)$
となります。
移項すると、
$f(x)g(x)=(f(x)g^*(x))’-f'(x)g^*(x)$
となります。
この両辺を積分すると、部分積分の公式が得られます。
部分積分の練習問題
部分積分を用いる不定積分の計算問題をたくさん紹介します。
例題1:$\displaystyle\int x\sin xdx$ を計算せよ。
$\displaystyle\int x\sin xdx\\
=x(-\cos x)-\displaystyle\int 1\cdot(-\cos x)dx\\
=-x\cos x+\sin x+C$
関連:xsinxの微分、グラフ、積分など
例題2:$\displaystyle\int (\log x)^2dx$ を計算せよ。
部分積分を2回使うことで、
$\displaystyle\int(\log x)^2=$$x(\log x)^2-2x\log x+2x+C$
が分かります。詳細はy=(logx)^2の微分、積分、グラフを参照してください。
例題3:$\displaystyle\int e^x\sin xdx$ を計算せよ。
例題4:$\displaystyle\int e^x\cos xdx$ を計算せよ。
求めたい積分を $I$ とおき、部分積分を2回使って $I$ に関する方程式を導きます。答えは
$\displaystyle\int e^x\sin xdx$$=\dfrac{1}{2}e^x(\sin x-\cos x)+C$
$\displaystyle\int e^x\cos xdx$$=\dfrac{1}{2}e^x(\sin x+\cos x)+C$
です。詳細はe^xsinxとe^xcosxの積分公式を参照してください。
ここからは高校数学の範囲外です。
例題5:$\displaystyle\int\mathrm{arcsin}\:xdx$ を計算せよ。
答えは、$x\mathrm{arcsin}\:x+\sqrt{1-x^2}+C$ です。
詳細はarcsinの意味、微分、不定積分の後半を参照してください。
例題6:$\displaystyle\int\mathrm{arccos}\:xdx$ を計算せよ。
答えは、$x\mathrm{arccos}\:x-\sqrt{1-x^2}+C$ です。
詳細はarccosの意味、微分、不定積分の後半を参照してください。
例題7:$\displaystyle\int\mathrm{arctan}\:xdx$ を計算せよ。
答えは、$x\mathrm{arctan}\:x-\dfrac{1}{2}\log(1+x^2)+C$ です。
詳細はarctanの意味、微分、不定積分の後半を参照してください。
例題8:$\displaystyle\int\sqrt{x^2+1}dx$ を計算せよ。
相当難しいです。答えは√x^2+1の積分を3ステップで分かりやすく解説を参照してください。
次回は 1/xの積分公式の証明、絶対値がつく理由 を解説します。
