不定積分(高校数学)
$\displaystyle\int xe^{-x}dx=-xe^{-x}-e^{-x}+C$
広義積分(大学数学)
$\displaystyle\int_0^{\infty}xe^{-x}dx=1$
$xe^{-x}$ の不定積分
まずは $xe^{-x}$ の不定積分を計算してみましょう。部分積分を使います。
部分積分について、基本的な使い方やコツを分かりやすく解説
$e^{-x}$ を積分すると $(-e^{-x})$ になるので、
$\displaystyle\int xe^{-x}dx\\
=x(-e^{-x})-\displaystyle\int (-e^{-x})dx\\
=-xe^{-x}+\displaystyle\int e^{-x}dx\\
=-xe^{-x}-e^{-x}+C$
となります。
$xe^{-x}$ の広義積分
次は、$0$ から無限大までの定積分(広義積分)を計算してみましょう。厳密には大学数学の範囲ですが、高校数学レベルでもだいたい理解できます。
$\displaystyle\int_0^{\infty}xe^{-x}$
とは
$\displaystyle\lim_{a\to\infty}\int_0^axe^{-x}dx$
のことです。
$0$ から $a$ までの定積分は(不定積分の結果を使うと)
$\left[-xe^{-x}-e^{-x}\right]_0^a\\
=-ae^{-a}-e^{-a}+1$
となります。最後に $a\to\infty$ の極限を取ると、上式は $1$ になります。
ただし、$\displaystyle\lim_{a\to\infty}ae^{-a}=0$ であることを使いました。
関連:極限の基本的な公式、考え方一覧
面積
$\displaystyle\int_0^{\infty}xe^{-x}dx=1$
という式の意味を、グラフで見てみましょう。
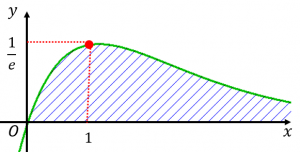
$y=xe^{-x}$ のグラフは図の緑色の線のようになるので、上の式は図の青色部分の面積が $1$ であることを表しています。グラフは右側に果てしなく続いていきますが、$xe^{-x}$ が $0$ に近づくスピードがはやいので、面積は有限の値を取るというわけです。
注:$y=xe^{-x}$ の導関数は $y=(1-x)e^{-x}$ なので、$x=1$ で最大値 $\dfrac{1}{e}$ を取ります。
次回は ガウス積分まわりの公式リスト を解説します。
