y=xe^xの微分、積分、グラフなど

微分

$y=xe^x$ を微分してみましょう。
積の微分公式：$(fg)’=f’g+fg’$ を使います：

$(xe^x)’\\
=(x)’e^x+x(e^x)’\\
=1\cdot e^x+x\cdot e^x\\
=e^x+xe^x\\
=(1+x)e^x$

となります。積の微分公式を使う最も典型的な例題です。→積の微分公式の頻出問題6問

積分

次は $xe^x$ です。異なる2種類の関数の積の積分には、部分積分を使います。
部分積分について、基本的な使い方やコツを分かりやすく解説

$x$ の微分は $1$、$e^x$ の積分は $e^x$ なので、
$\displaystyle\int xe^xdx\\
=xe^x-\displaystyle\int 1\cdot e^xdx\\
=xe^x-e^x+C$

となります。部分積分を使う最も典型的な例題です。

ちなみに、形は似ていますが、$\displaystyle\int xe^{x^2}$ の積分は部分積分ではできません。置換積分で計算します。→y=xe^x^2の積分、微分など

極限

$\displaystyle\lim_{x\to\infty}xe^x=\infty$ となるのはすぐ分かります。

一方、$x\to -\infty$ における $xe^x$ の極限値の計算には工夫が必要です。$y=-x$ と置換すると、
$\displaystyle\lim_{x\to -\infty}xe^{x}\\
=\displaystyle\lim_{y\to\infty}(-y)e^{(-y)}\\
=\displaystyle\lim_{y\to\infty}-\dfrac{y}{e^y}$
と変形できます。$y$ が十分大きいとき、$e^y$ は $y$ よりはるかに大きい（厳密には挟み撃ちの原理を使って証明する）ので、この式は $0$ に収束します。結局
$\displaystyle\lim_{x\to -\infty}xe^x=0$
となります。

漸近線、グラフ

$y=xe^x$ のグラフを書いてみます。

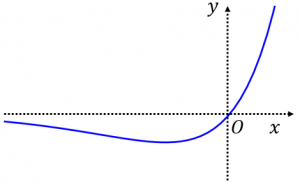
上記で計算した導関数：$y’=(1+x)e^x$ および極限に注意すると、グラフは図のようになります。

漸近線は、$x$ 軸（$y=0$）です。また、$x=-1$ で極小値 $-e^{-1}=-\dfrac{1}{e}$ を取ることが分かります。また、この極小値は最小値にもなっています。

次回は y=x^xの微分とグラフ を解説します。