arcsinの意味、微分、不定積分

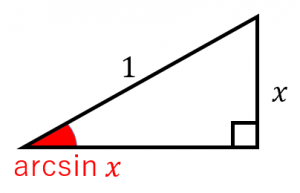
arcsinの意味、定義域、値域

$y=\sin x$（ただし、$-\frac{\pi}{2}\leq x\leq\frac{\pi}{2}$）の逆関数を $y=\mathrm{arcsin}\:x$ と書きます（ときどき $\mathrm{asin}\:x$ と書く人もいます）。

つまり $\mathrm{arcsin}\:x$ は、$\sin y=x$ となる $y$（で $-\frac{\pi}{2}\leq y\leq\frac{\pi}{2}$ を満たすもの）を返す関数です。

～定義域と値域～
$y=\mathrm{arcsin}\:x$ の定義域は、$-1\leq x\leq 1$、値域は $-\dfrac{\pi}{2}\leq y\leq\dfrac{\pi}{2}$ です。

arcsin xの微分

$y=\mathrm{arcsin}\:x$ の微分が $y’=\dfrac{1}{\sqrt{1-x^2}}$ であることを証明します。

逆関数の微分公式：$\dfrac{dx}{dy}=\dfrac{1}{\frac{dy}{dx}}$ を使います。

$y=\mathrm{arcsin}\:x$ は $x=\sin y$ と同じことです。この式の両辺を $y$ で微分すると、
$\dfrac{dx}{dy}=\cos y$
となります。よって（逆関数の微分公式より）、$\dfrac{dy}{dx}=\dfrac{1}{\cos y}$ です。

あとは、この右辺を $x$ で表してやります。$-\frac{\pi}{2}< y<\frac{\pi}{2}$ より、$\cos y> 0$ なので、
$\dfrac{1}{\cos y}=\dfrac{1}{\sqrt{1-\sin^2y}}\\
=\dfrac{1}{\sqrt{1-x^2}}$
となります。よって、$\dfrac{dy}{dx}=\dfrac{1}{\sqrt{1-x^2}}$ です。
→アークサイン、アークコサイン、アークタンジェントの微分

arcsin xの積分

$\displaystyle\int \mathrm{arcsin}\:xdx\\
=x\mathrm{arcsin}\:x+\sqrt{1-x^2}+C$

であることを証明します。

まず、部分積分と、arcsinの微分公式を使います（ここが一番難しいポイント）：
$\displaystyle\int \mathrm{arcsin}\:xdx\\
=\displaystyle\int 1\cdot\mathrm{arcsin}\:xdx\\
=x\mathrm{arcsin}\:x-\displaystyle\int x\cdot\dfrac{1}{\sqrt{1-x^2}}dx$

この第二項の積分は、$1-x^2=t$ と置換すると、$\frac{dt}{dx}=-2x$ なので、
$-\displaystyle\int x\cdot\dfrac{1}{\sqrt{t}}\dfrac{dt}{(-2x)}\\
=\dfrac{1}{2}\displaystyle\int t^{-\frac{1}{2}}dt\\
=t^{\frac{1}{2}}+C\\
=\sqrt{1-x^2}+C$
となります。

arcsin の微分を使って arcsin の積分をするというのがおもしろいです！

次回は arccosの意味、微分、不定積分 を解説します。