$(x\sin x)’=\sin x+x\cos x$
$\displaystyle\int x\sin xdx$$=-x\cos x+\sin x+C$
微分
$(x\sin x)’=\sin x+x\cos x$ であることを証明します。
積の微分公式:$(fg)’=f’g+fg’$ を使います。→積の微分公式の頻出問題6問
$(x\sin x)’\\
=x’\sin x+x(\sin x)’\\
=\sin x+x\cos x$
グラフ
$y=x\sin x$ のグラフの概形について考えます。
微分した式 $y’=\sin x+x\cos x$ は複雑で使い物になりません。増減表を利用してグラフを書くのは難しいです。
そこで、$\sin x$ が $-1$ から $1$ の間を周期的に変化していることに注意すると、$x\sin x$ のグラフは
$y=-x$ と $y=x$ の間を周期的に変化するような形になることが分かります。
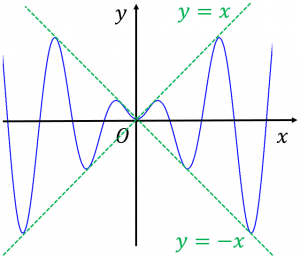
具体的には、$y=x$ と $y=-x$ のグラフ(緑色の点線)を書いてから、それらにつぶされた(押し広げられた) $\sin x$ のグラフを書くような感じです。
積分
$\displaystyle\int x\sin xdx$$=-x\cos x+\sin x+C$
であることを部分積分を用いて証明します。
$\sin x$ を積分すると $-\cos x$、
$x$ を微分すると $1$ なので、
$\displaystyle\int x\sin xdx\\
=x(-\cos x)-\displaystyle\int 1\cdot(-\cos x)dx\\
=-x\cos x+\sin x+C$
となります。
「多項式と三角関数の積の積分は部分積分を使う」と覚えておきましょう。
xsinxは偶関数
$f(x)=x\sin x$ とおくと、
$f(-x)=(-x)\sin (-x)\\
=x\sin x$
となるので、$f(x)$ は偶関数です。これを利用して定積分を簡単に計算することができます。
例:
$\displaystyle\int_{-\pi}^{\pi}x\sin xdx\\
=2\displaystyle\int_{0}^{\pi}x\sin xdx\\
=2[-x\cos x+\sin x]_0^{\pi}\\
=2\pi$
次回は xcosxの微分、グラフ、積分など を解説します。
