$\cos 72^{\circ}=\sin 18^{\circ}=\dfrac{\sqrt{5}-1}{4}\simeq 0.31$
弧度法で書くと、$\cos \dfrac{2\pi}{5}=\sin \dfrac{\pi}{10}=\dfrac{\sqrt{5}-1}{4}$
図形的に求める
まず、$\sin x=\cos(90^{\circ}-x)$ なので、$\sin 18^{\circ}=\cos 72^{\circ}$ であることが分かります。
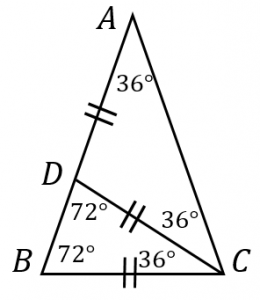
$AB=AC=1$、$\angle A=36^{\circ}$ $\angle B=\angle C=72^{\circ}$ である二等辺三角形 $ABC$ を考えます。$\angle C$ の二等分線を $CD$ とします。
三角形 $ABC$ と $CDB$ は全ての角度が等しいので相似です。
よって、$AB:BC=BC:BD$、つまり $AB\times BD=BC^2$ です。
これに、$AB=1$ と、$BD=AB-AD=1-DC=1-BC$ を代入すると、$1-BC=BC^2$ になります。この二次方程式を解くと、$BC=\dfrac{-1+\sqrt{5}}{2}$ となります($BC> 0$ を使った)。
よって、$\cos 72^{\circ}=\cos\angle B=\dfrac{BC}{2}=\dfrac{\sqrt{5}-1}{4}$ となります。
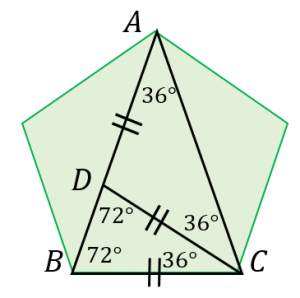
ちなみに、この二等辺三角形の頂点は正五角形の頂点のうち3つを選んだものです。
→正五角形の対角線の長さと高さ
方程式を解くことで求める
参考:2倍角の公式の証明と頻出例題
参考:sin、cos、tanの三倍角の公式の2通りの証明
$\theta=18^{\circ}$ とおくと、$5\theta=90^{\circ}$ です。これを変形すると、
$3\theta=90^{\circ}-2\theta$ です。
よって、$\sin 3\theta=\sin(90^{\circ}-2\theta)=\cos 2\theta$ となります。
この式の左辺は三倍角の公式より、$-4\sin^3\theta+3\sin\theta$
右辺は倍角の公式より $1-2\sin^2\theta$
と変形できます。
よって、
$-4\sin^3\theta+3\sin\theta=1-2\sin^2\theta$
が成立します。これを整理すると、
$4\sin^3\theta-2\sin^2\theta-3\sin\theta+1=0$
となります。これは $\sin\theta$ についての三次方程式です。$\sin\theta=1$ が解になっていることに注意すると、因数分解できます:
$(\sin\theta-1)(4\sin^2\theta +2\sin\theta-1)=0$
よって、$\sin\theta$ の候補は $1$、$\dfrac{-1\pm\sqrt{5}}{4}$
(→bが偶数の場合の解の公式)
となります。$\theta=18^{\circ}$ なので、$0 <\sin\theta <1$ です。よって、$\sin\theta=\dfrac{-1+\sqrt{5}}{4}$ となります。
次回は sin15度、cos15度、tan15度の値と求め方 を解説します。
