一辺の長さが $a$ の正五角形について、
対角線の長さは、$\dfrac{(\sqrt{5}+1)}{2}a\simeq 1.62a$
高さは、$\dfrac{a}{2}\sqrt{5+2\sqrt{5}}\simeq 1.54a$
対角線の長さ:前編
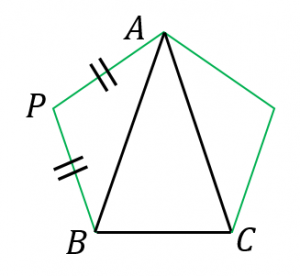
準備として、正五角形の頂点の一部からなる三角形 $ABC$ の角度が、$\angle A=36^{\circ}$、$\angle B=\angle C=72^{\circ}$ であることを確認してみます。
まず、正五角形の一つの内角の大きさは、$180\times (5-2)\div 5=108^{\circ}$ です。よって、$\angle PBA=(180-108)\div 2=36^{\circ}$ となります。
よって、$\angle ABC=108-36=72^{\circ}$ となります。対称性より、$\angle ACB=72^{\circ}$ です。また、$\angle BAC=180-72-72=36^{\circ}$ です。
対角線の長さ:後編
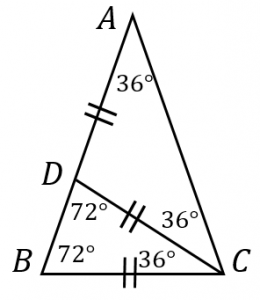
二等辺三角形 $ABC$ を切り出して考えます。
$\angle C$ の二等分線を $CD$ とします。
三角形 $ABC$ と $CDB$ は全ての角度が等しいので相似です。
よって、$AB:BC=BC:BD$、つまり $AB\times BD=BC^2$ です。
これに、$BC=a$ と、
$BD=AB-AD=AB-a$
を代入すると、$AB^2-aAB=a^2$ になります。この二次方程式($x^2-ax-a^2=0$)を解くと $AB=\dfrac{\sqrt{5}+1}{2}a$ となります($AB> 0$ を使った)。
なお、後編部分はcos72度、sin18度の2通りの求め方でやったこととほぼ同じです。
正五角形の高さ
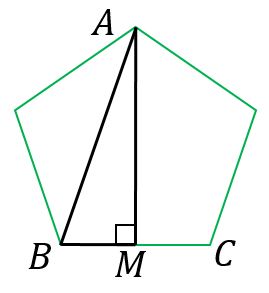
対角線 $AB$ の長さが分かってしまえば、高さ $AM$ を求めるのは簡単です。
三角形 $ABM$ に三平方の定理を使うと、
$AM^2=AB^2-BM^2\\
=\left(\dfrac{\sqrt{5}+1}{2}a\right)^2-\left(\dfrac{a}{2}\right)^2\\
=\dfrac{a^2(6+2\sqrt{5}-1)}{4}\\
=\dfrac{a^2}{4}(5+2\sqrt{5})$
よって、$AM=\dfrac{a}{2}\sqrt{5+2\sqrt{5}}$
次回は 正五角形の面積を求める2つの公式 を解説します。
