x+1/xの最小値の3通りの求め方
例題
$x+\dfrac{1}{x}$ の $x>0$ における最小値を求めよ。
解答1
相加平均、相乗平均の不等式より、
$x+\dfrac{1}{x}\geq 2\sqrt{x\cdot\dfrac{1}{x}}=2$
です。等号成立は $x=\dfrac{1}{x}$、つまり $x=1$ のときです。
よって答えは、$x=1$ のとき最小値 $2$ です。
関連:相加平均、相乗平均の不等式の意味と使い方
解答2
平方完成のような変形をします。
$x+\dfrac{1}{x}=\left(\sqrt{x}-\dfrac{1}{\sqrt{x}}\right)^2+2$
この右辺は「二乗+$2$」という形をしているので必ず $2$ 以上です。そして、$\sqrt{x}=\dfrac{1}{\sqrt{x}}$ のとき、つまり $x=1$ のときには $2$ になります。
よって、最小値は $2$ です。
関連:平方完成のやり方と練習問題を詳しく解説
解答3
微分してグラフを書くことでとりうる値の範囲(最小値も含む)を求めることができます(グラフの書き方は後述)。
グラフの書き方
例題2
$y=x+\dfrac{1}{x}$ のグラフの概形を書け。
解答
定義域は $x\neq 0$ です。
導関数は
$f’=1-\dfrac{1}{x^2}\\
=\dfrac{x^2-1}{x^2}=\dfrac{(x-1)(x+1)}{x^2}$
です。よって、
$-1 < x<1$ では微分がマイナスなので減少関数、それ以外では増加関数となります。
そして、
$x=1$ のときに極小値 $2$
$x=-1$ のときに極大値 $-2$
をとることが分かります。
また、極限は
$x\to\infty$ のとき $f(x)\to\infty$
$x\to -\infty$ のとき $f(x)\to -\infty$
$x\to +0$ のとき $f(x)\to\infty$
$x\to -0$ のとき $f(x)\to -\infty$
となります。
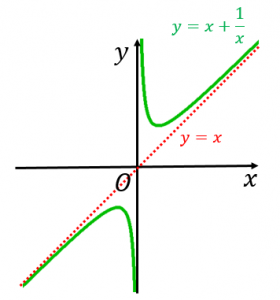
さらに、$x$ がとても大きい場合またはとても小さい場合は $\dfrac{1}{x}$ は無視できるので $x+\dfrac{1}{x}\simeq x$ となります。つまり、$y=x$ が漸近線です。
また、$x=0$($y$ 軸)も漸近線です。
以上のことに気をつけると、グラフは上図のようになります。とりうる値の範囲は $y\leq -2$、$2\leq y$ です。
補足、まめ知識
・$x+\dfrac{1}{x}$ は奇関数です。
・$\left(x+\dfrac{1}{x}\right)^2=x^2+\dfrac{1}{x^2}+2$ という等式は覚えておくとよいでしょう。実際、この式を知っていれば先程の解答2が思いつきやすいでしょう。
・$y=x+\dfrac{1}{x}$ のグラフは $y=x$ のグラフ(比例)と $y=\dfrac{1}{x}$ のグラフ(反比例)を足し合わせたようなグラフです。
関連:比例(数学)の意味を分かりやすく解説
関連:反比例の意味と身近な例4つ
次回は y=sinxcosxの微分、グラフ、積分 を解説します。
