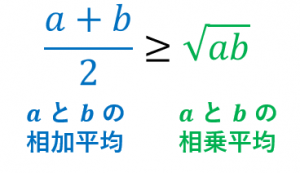
・$\dfrac{a+b}{2}$ のことを $a$ と $b$ の相加平均と言います。
・$\sqrt{ab}$ のことを $a$ と $b$ の相乗平均と言います。
・$a,b\geq 0$ のとき、相加平均は相乗平均以上です。つまり、
$\dfrac{a+b}{2}\geq\sqrt{ab}$
が成立します。
これを相加平均・相乗平均の不等式(または相加相乗平均の不等式、AM-GM不等式)と言います。
相加平均、相乗平均とは
二つの和を2で割ったもの $\dfrac{a+b}{2}$ を相加平均と言います。いわゆる普通の平均です。例えば、$5$ と $7$ の相加平均は、$\dfrac{5+7}{2}=6$ です。
二つの積のルートを取ったもの $\sqrt{ab}$ を相乗平均と言います。→相乗平均(幾何平均)の意味、図形的イメージ、活躍する例
例えば、$5$ と $7$ の相乗平均は、$\sqrt{5\times 7}=\sqrt{35}\simeq 5.916$ です。
確かに、$5$ と $7$ の相加平均は $5$ と $7$ の相乗平均より大きいです。
一般に、$a,b$ が $0$ 以上のとき、相加平均と相乗平均の間には、相加平均 $\geq$ 相乗平均という関係式が成立します。等号成立条件は $a=b$ です。
相加平均、相乗平均の不等式の証明
両辺を二倍した、
$a+b\geq 2\sqrt{ab}$
を証明すればOKです。
さらに、両辺を二乗した
$(a+b)^2\geq 4ab$
を証明すればOKです。
この式の左辺を展開して変形すると、
$a^2+2ab+b^2\geq 4ab$
$a^2-2ab+b^2\geq 0$
$(a-b)^2\geq 0$
となります。この最後の不等式は成立するので、確かにもとの不等式も成立することが分かります。そして、等号成立条件が $a=b$ であることも分かります。
使い方
例題
$x$ が正の実数全体を動くとき、$x+\dfrac{9}{4x}$ の最小値を求めよ。
解答
相加平均、相乗平均の不等式より、
$x+\dfrac{9}{4x}\geq 2\sqrt{x\cdot\dfrac{9}{4x}}\\
=2\sqrt{\dfrac{9}{4}}\\
=3$
等号成立条件は、$x=\dfrac{9}{4x}$ のとき、つまり$x^2=\dfrac{9}{4}$、$x=\dfrac{3}{2}$ のときである。
つまり、与えられた式は、$x=\dfrac{3}{2}$ のときに最小値 $3$ を取る。
次回は 相乗平均(幾何平均)の意味、図形的イメージ、活躍する例 を解説します。
