y=sinxcosxの微分、グラフ、積分

y=sinxcosxの微分

やり方その１
積の微分公式：$(fg)’=f’g+fg’$ （→積の微分公式の頻出問題6問）を使って導関数を計算します：
$(\sin x\cos x)’\\
=(\sin x)’\cos x+\sin x(\cos x)’\\
=\cos^2x-\sin^2x\\
=\cos 2x$
（最後に $\cos$ の倍角公式を用いました）
→2倍角の公式の証明と頻出例題

やり方その２
サインの倍角公式より、$\sin x\cos x=\dfrac{1}{2}\sin 2x$
なので、これを微分すると、
$\dfrac{1}{2}\cos 2x\cdot(2x)’\\
=\cos 2x$

y=sinxcosxのグラフ

$y=\sin x\cos x$ のグラフをいきなり書くのは難しいですが、サインの倍角公式を使って、$\sin x\cos x=\dfrac{1}{2}\sin 2x$ と変形すれば簡単にグラフを書くことができます。

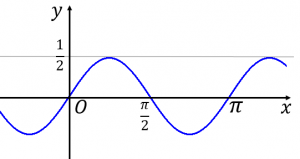
$y=\dfrac{1}{2}\sin 2x$ のグラフは周期が $\pi$、振幅（最大値）が $\dfrac{1}{2}$ であることに注意すると、図のようになります。

y=sinxcosxの不定積分

積分もサインの倍角公式を使って、$\sin x\cos x=\dfrac{1}{2}\sin 2x$ と変形すれば簡単です：

$\displaystyle\int \sin x\cos xdx\\
=\displaystyle\int\dfrac{1}{2}\sin 2xdx\\
=\dfrac{1}{2}\cdot\dfrac{1}{2}\cos 2x+C\\
=\dfrac{1}{4}\cos 2x+C$

まとめ

$y=\sin x\cos x$ という関数が登場したときは、とりあえずサインの二倍角の公式を使って $\dfrac{1}{2}\sin 2x$ という形に変形してから考えましょう！

次回は y=sinx+cosxの合成、グラフ、最大値など を解説します。