このページでは、
・平方完成とは何か?
・平方完成のやり方は?
・平方完成は何の役に立つのか?
といった、平方完成についての疑問にお答えします。3つのステップを覚えれば、どんな二次式も平方完成することができます!
平方完成とは
平方完成とは、
$x^2+6x$ = $(x+3)^2-9$
のように、二次式を $a(x-p)^2+q$ という形に変形することです。
実際、右辺を展開してみると、
$(x+3)^2-9=x^2+6x+9-9=x^2+6x$
となり、左辺と一致します。
平方完成のもう1つの例としては,
$-2x^2+12x-3$ = $-2(x-3)^2+15$
が挙げられます。こちらも、二次式を $a(x-p)^2+q$ という形に変形しています。
平方完成のやり方1
ステップ1.
まず、$x$ の係数の半分の二乗を足して引きます。
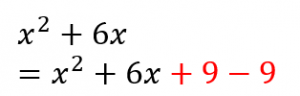
この場合、$x$ の係数は $6$ なので、$(6\div 2)^2=9$ を足して引きました。
ステップ2.
先頭の3つの項を二乗の形にまとめます。
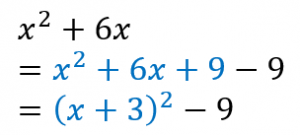
具体的には、$x^2+2ax+x^2=(x+a)^2$ という因数分解公式を使ってまとめます。
このように、$x^2$ の係数が $1$ のときは、以下の2ステップ:
1. $x$ の係数の半分の二乗を足して引く
2. 先頭の3つの項を二乗の形にまとめる
で平方完成できます。
平方完成のやり方2
$x^2$ の係数が $1$ でないときには、先ほどの2ステップに加えて、ステップ0が必要になります。
ステップ0.
まず、$x^2$ の係数で、最初の2項をくくります。
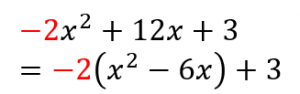
この場合、$x^2$ の係数は $-2$ なので、$-2$ でくくりました。
ステップ1.
次に、かっこの中身を見て$x$ の係数の半分の二乗を足して引きます。
この場合、$x$ の係数は $-6$ なので、$(-6\div 2)^2=9$ を足して引きました。
ステップ2.
かっこの中身を見て先頭の3つの項を二乗の形にまとめます。
これでほぼ完成です。最後に式を整理すると、
$-2\{(x-3)^2-9\}-3\\
=-2(x-3)^2+18-3\\
=-2(x-3)^2+15$
となります。
平方完成のやり方まとめ
ステップ0.$x^2$ の係数で、最初の2項をくくる。
ステップ1.$x$ の係数の半分の二乗を足して引く。
ステップ2.先頭の3つの項を二乗の形にまとめる(最後に式を整理する)
なぜ平方完成するのか?
なぜ平方完成するのか?
それは、平方完成は、二次関数のグラフを書いたり、二次方程式を解くために必要な式変形だからです。
平方完成の応用例1:
平方完成は、二次関数のグラフを書いて最大値を求める際に必要な式変形です。
→二次関数の最大値と最小値を求める問題4問
平方完成の応用例2:
平方完成は,二次方程式を解くために必要な式変形です。
→二次方程式の解の公式と問題4問
平方完成ができないと、二次関数や二次方程式の問題が解けません。そのため、平方完成のやり方は必ずマスターしましょう!
平方完成の練習問題
問題:
以下を平方完成せよ。
(1) $x^2+6x+7$
(2) $-x^2+3x+9$
(3) $3x^2-x+1$
解答:
(1)
$x^2+6x+7\\
=x^2+6x+9-9+7\\
=(x+3)^2-2$
途中で、一次の係数 6 の半分 3 の二乗である 9 を足して 9 を引きました。
(2)
$-x^2+3x+9\\
=-(x^2-3x)+9\\
=-(x^2-3x+\frac{9}{4}-\frac{9}{4})+9\\
=-\left\{(x-\frac{3}{2})^2-\frac{9}{4}\right\}+9\\
=-(x-\frac{3}{2})^2+\frac{9}{4}+9\\
=-(x-\frac{3}{2})^2+\frac{45}{4}$
途中で、カッコの中の一次の係数 $-3$ の半分 $-\frac{3}{2}$ の二乗である $\frac{9}{4}$ を足して $\frac{9}{4}$ を引きました。
(3)
$3x^2-x+1\\
=3(x^2-\frac{1}{3}x)+1\\
=3(x^2-\frac{1}{3}x+\frac{1}{36}-\frac{1}{36})+1\\
=3\left\{(x-\frac{1}{6})^2-\frac{1}{36}\right\}+1\\
=3(x-\frac{1}{6})^2-\frac{1}{12}+1\\
=3(x-\frac{1}{6})^2+\frac{11}{12}$
途中で、カッコの中の一次の係数 $-\frac{1}{3}$ の半分 $-\frac{1}{6}$ の二乗である $\frac{1}{36}$ を足して $\frac{1}{36}$ を引きました。
平方完成は、二次関数の最大値、最小値を求めたり、二次方程式を解くのに使う重要な式変形です。ぜひたくさん問題を解いてマスターしてください。
次回は 完全平方式の意味と例題2問 を解説します。
