比例関係
片方が $2$ 倍、$3$ 倍 $\cdots$ となると、もう片方も $2$ 倍、$3$ 倍となるような関係。
小学生でも分かる簡単な説明
二つの量について、片方が $2$ 倍、$3$ 倍 $\cdots$ となると、もう片方も $2$ 倍、$3$ 倍となるとき、その二つの量は比例関係にあると言います。
例1:$100$ グラムあたり $250$ 円のお肉が売っている。このとき、買うお肉の量と値段は比例関係にあります。
実際、買うお肉の量が $100$ グラムのときは $250$ 円ですが。
買う量を $2$ 倍にすると値段も $2$ 倍($500$ 円)、買う量を $3$ 倍にすると値段も $3$ 倍($750$ 円)になります。
ちなみに、反比例については反比例の意味と身近な例を参照してください。
数式、グラフによる説明
~数式による説明~
二つの量 $x$ と $y$ が、$y=ax$ という関係にあるとき、$x$ と $y$ は比例関係にある($y$ は $x$ に比例する)と言います。
~グラフによる説明~
$x$ と $y$ の関係をグラフに表したとき、原点を通る直線になるとき、$x$ と $y$ は比例関係にある($y$ は $x$ に比例する)と言います。
さきほどの例1を数式、グラフで説明してみます。
例1:$100$ グラムあたり $250$ 円のお肉が売っている。買うお肉の量と値段は比例します。
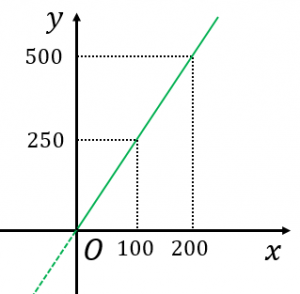
買うお肉の量を $x$(グラム)、値段を $y$(円)とします。このとき、$y=2.5x$ という関係式が成立します。
また、$x$ と $y$ の関係をグラフに表すと、図のようになります。
比例定数がマイナスの場合の例
数式による説明で登場した式 $y=ax$ の $a$ を比例定数と言います。お肉の例では比例定数は $2.5$ でした。比例定数が負になるような場合もあるので、そのような具体例を紹介します。
例2:最近雨が降らず、毎日 $2\:\mathrm{cm}$ ずつ川の水位が減少している。このとき経過した日数と水位の増加量は比例関係にあります。
経過した日数が $2$ 倍、$3$ 倍 $\cdots$ となると、水位の増加量も $2$ 倍、$3$ 倍となります。
数式で表すと、$y=-2x$ という関係が成立します。
($x$ は経過した日数、$y$ は水位の増加量)
比例定数は $-2$ となり、マイナスの値です。
次回は 比例定数の意味と求め方 を解説します。
