y=x^xの微分とグラフ

このページでは、$y=x^x$ という関数のいろいろな性質を見ていきます。

y=x^xの微分

$y=x^x$ について、定義域は $x>0$ なので、$x^x > 0$ となります。
そこで、両辺の対数を取ると、
$\log y=x\log x$
となります。

この両辺を $x$ で微分すると、
$\dfrac{y’}{y}=\log x +1$
となります。よって、
$y’=y(\log x +1)$
$=x^x(\log x+1)$
となります。

$y=x^x$ のグラフ

$y’=x^x(\log x+1)=0$
となるのは、$\log x=-1$ のとき、つまり、$x=\dfrac{1}{e}$ のときです。

導関数の符号に注意すると、
$0 < x < \dfrac{1}{e}$ では $y$ は減少
$\dfrac{1}{e} < x$ では $y$ は増加
となります。

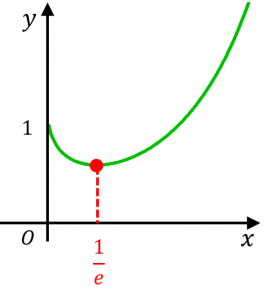
よって、グラフは図のようになります（定義域は $x > 0$ です）。極小値（かつ最小値）は、$\left(\dfrac{1}{e}\right)^{\frac{1}{e}}\fallingdotseq 0.69$
です。

ただし、$\displaystyle\lim_{x\to + 0}x^x=1$
であることを使いました。（証明は後述します）

極限

まず、極限の基本的な公式、考え方一覧 の９を使うと、
$\displaystyle\lim_{y\to\infty}\dfrac{-\log y}{y}=0$
であることが分かります。

この式で $\dfrac{1}{y}=x$ とすると、
$\displaystyle\lim_{x\to +0}x\log x=0$
となります。これを変形していくと、
$\displaystyle\lim_{x\to +0}\log x^x=0$
$\displaystyle\lim_{x\to +0}x^x=1$
となります。

積分

wolframalpha.comにアクセスし、
integral of x^x
と入力してみましたが、no results found と返ってきました。

$x^x$ の原始関数を初等的な関数で表すのは（不可能かどうかは分かりませんが）難しそうです。

次回は y=(logx)^2の微分、積分、グラフ を解説します。