三角錐、四角錐、円錐の体積を求める公式と例題

三角錐の体積を計算する

まずは底面積を計算してみましょう。底面は $\angle BCD=90^{\circ}$ である直角三角形なので、面積は
$3\times 2\div 2=3\:\mathrm{cm^2}$
となります。

また、この場合の高さは $AC=4\:\mathrm{cm}$ となります。

よって、三角錐の体積は、
$\dfrac{1}{3}$×(底面積)×(高さ)
$=\dfrac{1}{3}\times$$3$$\times$$4$
$=4\:\mathrm{cm^3}$
となります。

この問題は高さがすぐに求まりましたが、高さを頑張って計算しないといけない問題もあります。
関連：正四面体の高さと体積の求め方

四角錐の体積を計算する

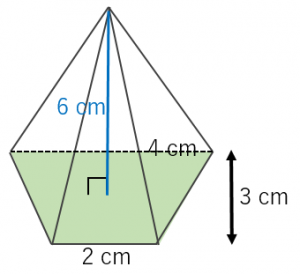
まずは底面積を計算してみましょう。底面は台形なので台形の面積を求める公式より、面積は
$(4+2)\times 3\div 2=9\:\mathrm{cm^2}$
となります。

また、この場合の高さは $6\:\mathrm{cm}$ となります。

よって、四角錐の体積は、
$\dfrac{1}{3}$×(底面積)×(高さ)
$=\dfrac{1}{3}\times$$9$$\times$$6$
$=18\:\mathrm{cm^3}$
となります。

円錐の体積を計算する

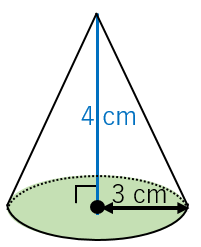
まずは底面積を計算してみましょう。底面は円なので、面積は
$3\times 3\times \pi=9\pi\:\mathrm{cm^2}$
となります。

また、高さは $4\:\mathrm{cm}$ です。

よって、円錐の体積は、
$\dfrac{1}{3}$×(底面積)×(高さ)
$=\dfrac{1}{3}\times$$9\pi$$\times$$4$
$=12\pi\:\mathrm{cm^3}$
となります。

関連：円錐の側面積、底面積、表面積の求め方

次回は 外径と内径の意味と厚さの計算例 を解説します。