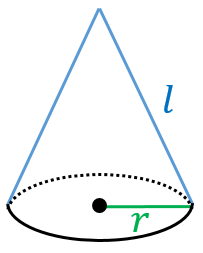
底面の半径が $r$、母線の長さが $l$ の円錐について、
側面積は $\pi rl$
底面積は $\pi r^2$
表面積は $\pi rl+\pi r^2$
簡単な具体例(公式を使って計算する)
例題
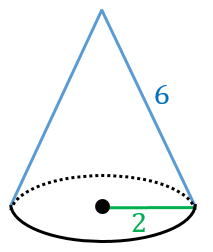
底面の半径が $2$、母線の長さが $6$ の円錐について、側面積、底面積、表面積をそれぞれ計算せよ。
解答
側面積は公式より、
(円周率)×(底面の半径)×(母線の長さ)
$=\pi\times 2\times 6$
$=12\pi$
となります。
底面積は、半径が $2$ の円の面積なので、
$\pi\times 2^2$
$=4\pi$
となります。
表面積は側面積と底面積の和なので、
$12\pi+4\pi$
$=16\pi$
となります。
側面積の求め方(公式を使わない)
公式を忘れても計算できるように、公式を使わない方法も紹介しておきます。
例題の別解
円錐の展開図を書いてみましょう。すると、側面はおうぎ形になります。おうぎ形の面積を計算するためには、中心角が必要になります。中心角を $x^{\circ}$ とすると、赤い弧の長さは $2\pi \cdot 6\times\dfrac{x}{360}=\dfrac{x\pi}{30}$ です。
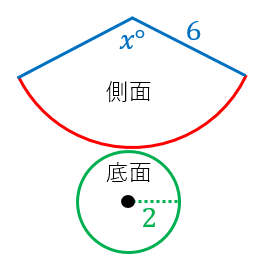
一方、底面の円周の長さは $2\pi \cdot 2=4\pi$ です。
展開図はくっつけられるはずなので、赤と緑の長さは等しいです。よって、
$4\pi=\dfrac{x\pi}{30}$
よって、$x=120^{\circ}$ です。
おうぎ形の中心角が $120^{\circ}$ であることが分かったので側面積は、
$\pi \cdot 6^2\times\dfrac{120}{360}\\
=\pi \cdot 36\times\dfrac{1}{3}\\
=12\pi$
と計算できます。
公式の証明
側面積が $\pi rl$ になることを証明してみましょう。上記の別解と同様に、円錐の展開図を書いてみましょう。
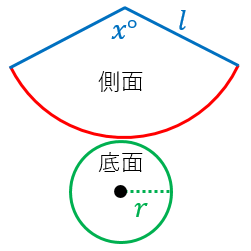
中心角を $x^{\circ}$ とすると、赤い弧の長さは $2\pi l\times\dfrac{x}{360}$ です。
一方、底面の円周の長さは $2\pi r$ です。
赤と緑の長さは等しいので、
$2\pi r=2\pi l\times\dfrac{x}{360}$
$r=l\times\dfrac{x}{360}$
よって、$\dfrac{x}{360}=\dfrac{r}{l}$
になります。
中心角 $x$ が分かったので側面積 $S$ が分かります:
$S=\pi l^2\times\dfrac{x}{360}\\
=\pi l^2\times\dfrac{r}{l}\\
=\pi rl$
底面積は簡単です。半径 $r$ の円なので、面積は $\pi r^2$ になります。
そして、表面積は側面積+底面積なので、$\pi rl+\pi r^2$ になります。
次回は 円錐の母線、半径、中心角の関係式とそれぞれの求め方 を解説します。
