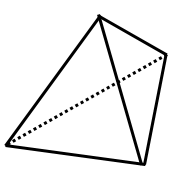
一辺の長さが $a$ である正四面体(4つの面全てが正三角形である四面体)について
高さは、$\dfrac{\sqrt{6}}{3}a$
体積は、$\dfrac{\sqrt{2}}{12}a^3$
断面図を用いて高さを求める
正四面体の高さ、つまり $AH$ の長さを計算します。($H$ は $A$ から $BCD$ に下ろした垂線の足)
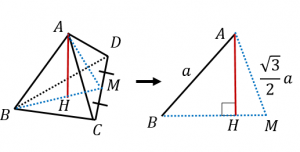
正四面体を $ABH$ を含む平面で切ってみます。この平面は(対称性より) $CD$ の中点 $M$ を含みます。そこで、三角形 $ABM$ を切り出してみます。$AB=a$、$AM=BM=\dfrac{\sqrt{3}}{2}a$ となります。
$AH=h$ とおくと、三平方の定理より、
$\sqrt{a^2-h^2}+\sqrt{\frac{3}{4}a^2-h^2}\\
=BH+HM=BM=\frac{\sqrt{3}}{2}a$
ここで、$\sqrt{a^2-h^2}$ を移項して両辺二乗すると、
$\frac{3}{4}a^2-h^2$
$=\frac{3}{4}a^2+(a^2-h^2)-\sqrt{3}a\sqrt{a^2-h^2}$
移項して両辺 $a$ で割ると、$\sqrt{3}\sqrt{a^2-h^2}=a$
もう一度両辺を二乗すると、
$3a^2-3h^2=a^2$
$h^2=\frac{2}{3}a^2$
$h=\dfrac{\sqrt{6}}{3}a$ となります。
注:他にもいろいろな方法があります。
体積を求める
一辺が $a$ の正四面体の底面は、一辺が $a$ の正三角形なので、底面積は $\dfrac{\sqrt{3}}{4}a^2$ です。
→正三角形の面積の求め方(小学生用~高校生用)
底面積と高さが求まったので、体積 $V$ は以下のように計算できます:
$V=\dfrac{\sqrt{3}}{4}a^2\cdot\dfrac{\sqrt{6}}{3}a \cdot\dfrac{1}{3}$
$=\dfrac{\sqrt{2}}{12}a^3$
立方体を用いた裏ワザ
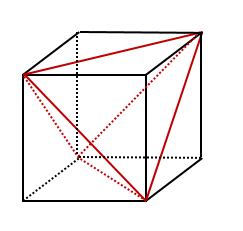
一辺が $a$ の正四面体は、
一辺が $\dfrac{a}{\sqrt{2}}$ である立方体から
「縦、横、高さが全て $\dfrac{a}{\sqrt{2}}$ である直角三角錐」を4つ引いたもの(図をじっくり見て理解してください!)なので、体積は、
$\left(\dfrac{a}{\sqrt{2}}\right)^3-4\cdot\dfrac{a}{\sqrt{2}}\cdot\dfrac{a}{\sqrt{2}}\cdot\dfrac{1}{2}\cdot\dfrac{a}{\sqrt{2}}\cdot\dfrac{1}{3}\\
=\dfrac{a^3}{2\sqrt{2}}-\dfrac{a^3}{3\sqrt{2}}\\
=\dfrac{\sqrt{2}}{4}a^3-\dfrac{\sqrt{2}}{6}a^3$
$=\dfrac{\sqrt{2}}{12}a^3$
正四面体の底面積は $\dfrac{\sqrt{3}}{4}a^2$ なので、
$\dfrac{\sqrt{2}}{12}a^3=\dfrac{\sqrt{3}}{4}a^2\cdot h\cdot\dfrac{1}{3}$
よって、$h=\dfrac{\sqrt{2}}{\sqrt{3}}=\dfrac{\sqrt{6}}{3}$
次回は 図形の面積を求める公式たち19個 を解説します。
