最終更新日 2018/12/28
「外側の円」の直径のことを外径と言います。
「内側の円」の直径のことを内径と言います。
外径と内径
「外側の円」と「内側の円」が考えられるような物体について、外径や内径が定まります。
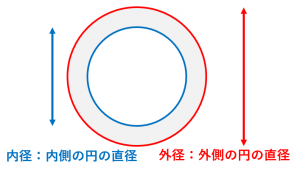
例えば、厚みのある円柱(パイプ)を考えてみましょう。パイプの断面図を見ると、外側の円と内側の円があります。この外側の円の直径を外径、内側の円の直径を内径と呼ぶことが多いです。
外径や内径は、半径ではなく、直径であることに注意してください。
また、厚みのある円柱だけでなく、厚みのある球についても、断面図(球の中心を通る平面で切った図)は上図のようになるので、同様に外径と内径と呼ばれることがあります。
外径、内径、厚さの関係
外径=内径+厚さ+厚さという公式が成立します。
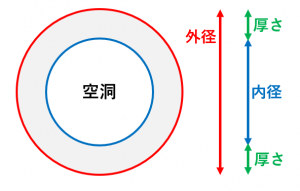
外径は、厚さの部分を2回通過するため、上記の公式が成立します。
そのため、外径、内径、厚さという3つの長さのうち、2つが分かれば残りの1つも計算できます。
計算問題の例
内径が $10\:\mathrm{cm}$、厚さが $2\:\mathrm{cm}$ のパイプの外径を計算してみましょう。
外径=内径+厚さ+厚さ
なので、外径は
$10+2+2=14\:\mathrm{cm}$
となります。
外径が $20\:\mathrm{cm}$、厚さが $3\:\mathrm{cm}$ のパイプの内径を計算してみましょう。
公式を変形すると、
内径=外径ー厚さー厚さ
となるので、内径は
$20-3-3=14\:\mathrm{cm}$
となります。
外径が $60\:\mathrm{cm}$、内径が $40\:\mathrm{cm}$ のパイプの厚さを計算してみましょう。
公式を変形すると、
厚さ=(外径ー内径)÷2
となるので、厚さは
$(60-40)\div 2=10\:\mathrm{cm}$
となります。
注意点
内径という言葉が「内側の円の直径」ではなく「内側の円の円周の長さ」という意味で使われる場合もあるので注意が必要です。
※ただし「内側の円の直径」という意味で使われることの方が多いと思われます。
次回は 前年比と増減率の計算方法と落とし穴 を解説します。
