台形の面積は、
(上底+下底)× 高さ ÷ 2
で計算することができます。
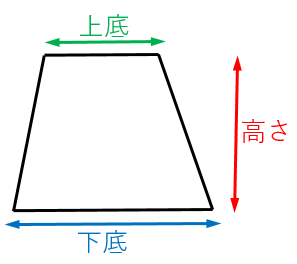
このページでは、台形の面積の求め方について詳しく解説します。
台形の面積を求める例題
台形の面積を求める公式
(上底+下底)× 高さ ÷ 2
を使って台形の面積を計算してみましょう。
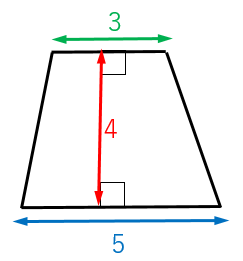
例題の答え
台形の面積公式より
(上底+下底)× 高さ ÷ 2
$=(3+5)\times 4\div 2=16\:\mathrm{cm}^2$
が答えとなります。
台形の面積公式の証明
台形の面積を求める公式
(上底+下底)× 高さ ÷ 2
を証明してみましょう。
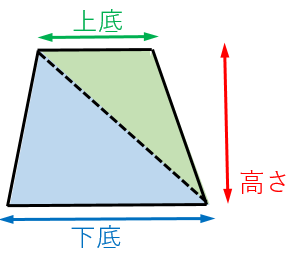
緑の三角形の面積は、三角形の面積公式より、
上底 × 高さ ÷ 2
青い三角形の面積は、三角形の面積公式より、
下底 × 高さ ÷ 2
台形の面積はこれら2つを足し合わせることで、
(上底+下底)× 高さ ÷ 2
となります。
公式を忘れてしまっても大丈夫
台形の面積公式は、三角形の面積公式(底辺 × 高さ ÷ 2)がもとになっています。
もし台形の面積公式を忘れてしまっても、対角線を引いて2つの三角形に分けて計算するという原理を覚えていれば、すぐに公式は導けるので問題ありません。
つまり、この公式はそこまで重要な公式ではないのです。そのため、小学校で台形の面積公式を習っていない方もいるかもしれません。ですが、時間の節約になるので覚えておくことをオススメします。
応用問題
例題2
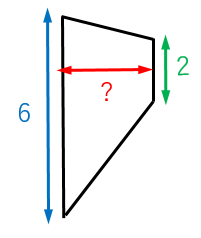
図のような横向きの台形について、面積は $12$ であったとする。この台形の高さ(図の横幅)を計算せよ。
答え
台形が横向きになっていますが、
上底 = 2
下底 = 6
と考えることができます。そこで、台形の高さを $x$ とおくと、台形の面積は、
(上底+下底)× 高さ ÷ 2
$=(2+6)\times x\div 2\\
=4x$
となります。
問題文の条件より、これが $12$ と等しいので $4x=12$ つまり $x=3$ であることが分かります。
この例題のように、台形が横向きになっていても、傾いていても考え方は同じです。(上底+下底)の部分は平行な2つの辺の長さの和と覚えるのがよいかもしれません。
次回は ひし形の面積を求める方法と例題 を解説します。
