正八面体は、図のような、正三角形 $8$ 枚で構成される正多面体です。
以下、正八面体の一辺の長さを $a$ として、いろいろな量を計算してみます。
体積
正八面体の頂点6つを、図のように $A$ から $F$ とします。
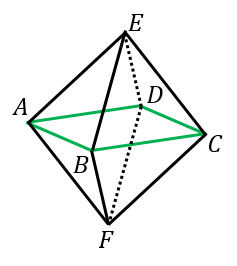
・$ABCD$ は一辺の長さが $a$ の正方形です。
・$EF$ は、一辺の長さが $a$ の正方形 $BEDF$ の対角線なので、$EF=\sqrt{2}a$ です。また、点 $E$ と $ABCD$ の距離は、$EF$ の長さの半分なので、$\sqrt{2}a\div 2=\dfrac{\sqrt{2}}{2}a$ です。
これらに注意すると、上半分(底面が $ABCD$ でもう1つの頂点が $E$ である正四角錐)の体積は、
$a^2\times\dfrac{\sqrt{2}}{2}a\times\dfrac{1}{3}=\dfrac{\sqrt{2}}{6}a^3$
同様に、下半分の体積も $\dfrac{\sqrt{2}}{6}a^3$
となります。
よって、正八面体の体積は、
$\dfrac{\sqrt{2}}{6}a^3\times 2$ $=\dfrac{\sqrt{2}}{3}a^3$
表面積
一辺の長さが $a$ の正三角形の面積は、$\dfrac{\sqrt{3}}{4}a^2$ です。
→正三角形の面積の求め方(小学生用~高校生用)
よって、正八面体の表面積は、
$\dfrac{\sqrt{3}}{4}a^2\times 8$ $=2\sqrt{3}a^2$
外接球の半径
正八面体の6つの頂点全てを通る球(外接球)の半径を求めてみましょう。
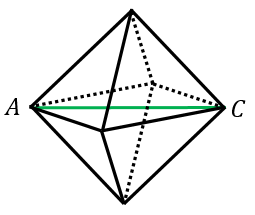
$AC$ は、外接球の直径になっています。
体積を求める際に計算したように、$AC=\sqrt{2}a$ なので、
(→正方形の対角線の長さを求める方法)
外接球の半径は、$\dfrac{\sqrt{2}}{2}a$ となります。
内接球の半径
正八面体の8つの面全てに接する球(内接球)の半径 $r$ を求めてみましょう。これが一番むずかしいです。正八面体の体積を2通りの方法で表します。
方法1:
さきほど計算したもの。$\dfrac{\sqrt{2}}{3}a^3$
方法2:
正八面体を「1つの面を底面として、正八面体の中心をもう一つの頂点とするような三角錐」が8つ集まったもの
とみなします。すると、正八面体の体積は、
$\dfrac{\sqrt{3}}{4}a^2\times r\times\dfrac{1}{3}\times 8=\dfrac{2\sqrt{3}}{3}a^2r$
となります。
よって、
$\dfrac{\sqrt{2}}{3}a^3=\dfrac{2\sqrt{3}}{3}a^2r$
となります。
これを $r$ について解くと、
$r=a\times\dfrac{\sqrt{2}}{3}\div\dfrac{2}{3}\sqrt{3}$
$=\dfrac{\sqrt{6}}{6}a$
となります。
次回は 正四面体の高さと体積の求め方 を解説します。
