正方形の対角線の長さを求める方法

具体例

例題

1辺の長さが $10\:\mathrm{cm}$ である正方形の対角線の長さを計算せよ。

解答

(対角線の長さ)$=$(1辺の長さ)$\times\sqrt{2}$
なので、$10\sqrt{2}\:\mathrm{cm}$ が対角線の長さになります。

$\sqrt{2}$（二乗して2になる数）はだいたい $1.414$ なので、おおよその長さは $10\times 1.414=14.14\:\mathrm{cm}$ と求めることができます。

計算ツール

1辺の長さを入力して「計算する」を押すと正方形の一辺の長さを計算してくれます。

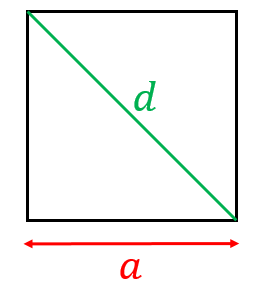
公式が成り立つ理由

最後に公式を証明します。中学数学で習う三平方の定理（ピタゴラスの定理）を使います。

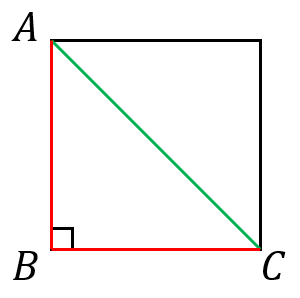
図において、三角形 $ABC$ は直角三角形なので、三平方の定理より
$AB^2+BC^2=AC^2$
(1辺)${}^2+$(1辺)${}^2=$(対角線)${}^2$
(1辺)${}^2\times\sqrt{2}=$(対角線)${}^2$

両辺のルートを取ると、
(対角線)$=$(1辺)$\times\sqrt{2}$
となります。

$\sqrt{2}$ は二乗して $2$ になる数で、その値はおおよそ $1.414$ です。
（$1.414^2=1.999396$）

関連：正方形の面積を求める2つの公式

次回は 長方形の対角線の長さの求め方 を解説します。