正三角形の面積の求め方（小学生用～高校生用）

正三角形の面積公式の証明（中学数学）

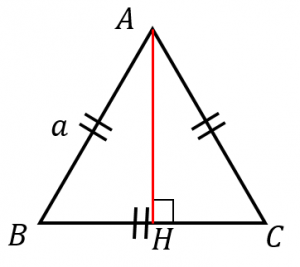
$H$ は $BC$ の中点なので、$BH=\dfrac{1}{2}a$ です。よって、三角形 $ABH$ に三平方の定理を使うと、
$AH^2=AB^2-BH^2\\
=a^2-\left(\dfrac{a}{2}\right)^2=\dfrac{3}{4}a^2$

よって、正三角形の面積は、
$\dfrac{1}{2}\times BC\times AH\\
=\dfrac{1}{2}a\cdot\dfrac{\sqrt{3}}{2}a=\dfrac{\sqrt{3}}{4}a^2$
となります。

正三角形の面積公式の証明（高校数学）

よって、一辺が $a$ の正三角形の面積は、
$S=\dfrac{1}{2}a\cdot a\cdot \sin 60^{\circ}\\
=\dfrac{1}{2}a^2\cdot\dfrac{\sqrt{3}}{2}\\
=\dfrac{\sqrt{3}}{4}a^2$

補足：この公式を使えば正四面体の体積を計算できます。→正四面体の高さと体積の求め方

関連：図形の面積を求める公式たち19個

小学生でも分かる公式

先ほど、正三角形の面積は $\dfrac{\sqrt{3}}{4}a^2$ であることを証明しました。この公式と、
$\dfrac{\sqrt{3}}{4}=0.4330127\cdots$
であることを使えば、
（一辺の長さ）×（一辺の長さ）×$0.43$
が分かります。

より正確な値を知りたい人は、$0.43\to 0.433$ とすればよいでしょう。

余談ですが、これは円の面積がおおよそ
（半径）×（半径）× $3.14$
である、という公式と似ています。

正三角形の面積を計算する例題

答え（小学生向け）

面積は、
（一辺の長さ）×（一辺の長さ）×$0.43$
$=4\times 4\times 0.43$
$=6.88\:\mathrm{cm}^2$

答え（厳密な値）

面積は、
$\dfrac{\sqrt{3}}{4}\times 4^2$
$=4\sqrt{3}\:\mathrm{cm}^2$

ちなみに、$4\sqrt{3}=6.9282\cdots$
です。

次回は 四角形の対角線の長さから面積を求める公式 を解説します。