正五角形の面積を求める2つの公式

中心から頂点までの距離が分かっている場合

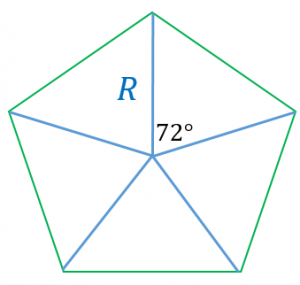
図のように、正五角形を5つの合同な三角形に分割します。5つの三角形は頂角が $360\div 5=72^{\circ}$ の二等辺三角形なので、その面積は、
$T=\dfrac{1}{2}\cdot R^2\sin 72^{\circ}$
です。

次に、$\cos 72^{\circ}=\dfrac{\sqrt{5}-1}{4}$ であること（これは有名なので覚えておきましょう、証明は→cos72度、sin18度の2通りの求め方をどうぞ）を用いて　$\sin 72^{\circ}$ を計算します：

$\sin 72^{\circ}=\sqrt{1-\left(\dfrac{\sqrt{5}-1}{4}\right)^2}\\
=\dfrac{1}{4}\sqrt{16-5+2\sqrt{5}-1}\\
=\dfrac{1}{4}\sqrt{10+2\sqrt{5}}$

よって、正五角形の面積は、
$5T=\dfrac{5R^2}{2}\times\dfrac{1}{4}\sqrt{10+2\sqrt{5}}\\
=\dfrac{5R^2}{8}\sqrt{10+2\sqrt{5}}$

一辺の長さが分かっている場合

中心から頂点までの距離を $R$ とします。

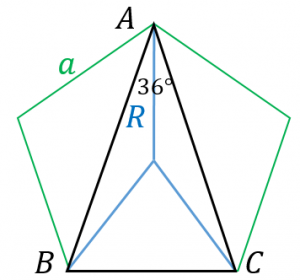
三角形 $ABC$ に正弦定理を使うと（→正弦定理を使う例題2問と証明）$\dfrac{a}{\sin 36^{\circ}}=2R$ となります。

よって「中心から頂点までの距離が分かっている場合」の公式に $R=\dfrac{a}{2\sin 36^{\circ}}$ を代入すると、求める面積は、
$S=\dfrac{5}{8}\sqrt{10+2\sqrt{5}}\cdot\dfrac{a^2}{4\sin^2 36^{\circ}}$
となります。さらに、半角の公式を使うと、$4\sin^2 36^{\circ}=2-2\cos 72^{\circ}=\dfrac{5-\sqrt{5}}{2}$ なので、

$S=\dfrac{5a^2}{8}\sqrt{10+2\sqrt{5}}\cdot\dfrac{2}{5-\sqrt{5}}\\
=\cdots\\
=\dfrac{a^2}{4}\sqrt{25+10\sqrt{5}}$

なお、最後の計算は省略しましたが、少しめんどくさいです。分母の有理化をしてから $\dfrac{a^2}{4}$ 以外を全部ルートの中に押しこんで計算します。

関連：図形の面積を求める公式たち19個

次回は cos72度、sin18度の2通りの求め方 を解説します。