どのような三角形 $ABC$ に対しても、
$\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}=2R$
が成立する。
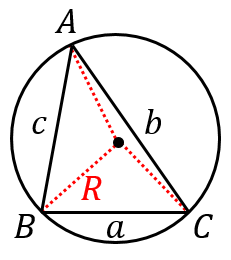
ただし、$A$ は $\angle A$ の大きさ、$a$ は辺 $BC$ の長さ(他も同様、図参照)。また、$R$ は三角形 $ABC$ の外接円の半径。
正弦定理を使う例題2問
問題1
三角形 $ABC$ について、$A=45^{\circ}$、$B=60^{\circ}$、$a=3$ であるとき、$b$ を求めよ。
解答
正弦定理より、$\dfrac{a}{\sin A}=\dfrac{b}{\sin B}$
与えられた条件を代入すると、$\dfrac{3}{\sin 45^{\circ}}=\dfrac{b}{\sin 60^{\circ}}$
よって、$\dfrac{6}{\sqrt{2}}=\dfrac{2b}{\sqrt{3}}$
$b=\dfrac{\sqrt{3}}{2}\cdot\dfrac{6}{\sqrt{2}}$$=\dfrac{3}{2}\sqrt{6}$
問題2
問題2:三角形 $ABC$ について、$A=45^{\circ}$、$a=3$ であるとき、外接円の半径 $R$ を計算せよ。
解答
正弦定理より、$\dfrac{a}{\sin A}=2R$
与えられた条件を代入すると、$\dfrac{3}{\sin 45^{\circ}}=2R$
よって、$R=\dfrac{3}{2}\cdot\dfrac{1}{\sin 45^{\circ}}$$=\dfrac{3}{2}\sqrt{2}$
正弦定理の証明
$\dfrac{a}{\sin A}=2R$ を証明します。これさえできれば、$\dfrac{b}{\sin B}=2R$、$\dfrac{c}{\sin C}=2R$ も同様に(対称性より)証明されるので、正弦定理が証明できたことになります。
三角形 $ABC$ の外接円の中心(外心)を $O$ とおきます。また、$O$ から $BC$ に下ろした垂線の足を $M$ とします。
$\angle A<90^{\circ}$ のとき
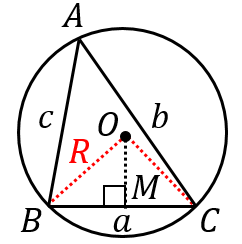
中心角は円周角の半分なので、
$\angle BOM=\dfrac{1}{2}\angle BOC=\angle A$
よって、$a=2BM=2OB\sin\angle BOM$$=2R\sin A$
つまり、$\dfrac{a}{\sin A}=2R$
$\angle A=90^{\circ}$ のとき
$BC$ が直径なので、$a=2R$ である。これと、$\sin A=\sin 90^{\circ}=1$ より正弦定理:$\dfrac{a}{\sin A}=2R$ は正しい。
$\angle A>90^{\circ}$ のとき
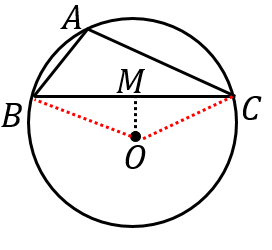
同様に、円周角と中心角の関係から、$\angle BOM=180^{\circ}-A$
よって、$a=2BM=2OB\sin\angle BOM$$=2R\sin A$
(ここで、$\sin A=\sin 180^{\circ}-A$ を用いました)
次回は 余弦定理の証明と例題 を解説します。
