複素数平面について、定義から難しい公式まで16個の知識

複素数平面について、複素数平面の定義や足し算引き算など簡単な公式から、ド・モアブルの定理や1のn乗根など難しい公式まで16個を整理しました。

複素数平面とは

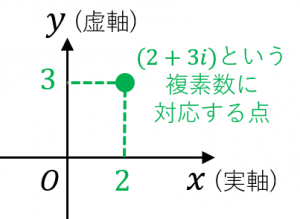
例えば、$(2+3i)$ という複素数は、原点から右に $2$、上に $3$ 移動した点に対応します。全ての複素数が、平面上の１つの点に対応します。

複素数平面のことをガウス平面と呼ぶことがあります。また、横軸を実軸、縦軸のことを虚軸と呼びます。

複素数平面における足し算

２つの複素数 $z_1,z_2$ に対して、
$z_1+z_2$ に対応する点は、原点から $z_1$ と $z_2$ に対応する点へのベクトルを加えたものに対応します。原点、$z_1$、$z_2$、$z_1+z_2$ の４点で平行四辺形になります。

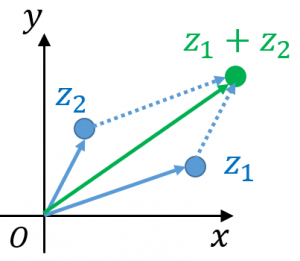
成分で表すと、$z_1=x_1+iy_1$、$z_2=x_2+iy_2$ のとき、$z_1+z_2=(x_1+x_2)+i(y_1+y_2)$ となります。

複素数平面における引き算

２つの複素数 $z_1,z_2$ に対して、
$z_1-z_2$ に対応する点は、原点から $z_1$ と $-z_2$ に対応する点へのベクトルを加えたものに対応します。$z_2$ を逆向きにしてから平行四辺形を作るイメージです。

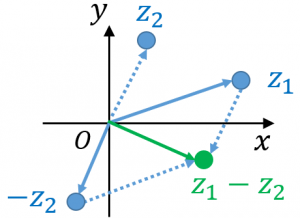
成分で表すと、$z_1=x_1+iy_1$、$z_2=x_2+iy_2$ のとき、$z_1-z_2=(x_1-x_2)+i(y_1-y_2)$ となります。

複素数平面内での対称移動

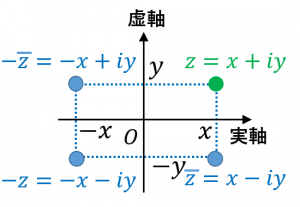
ただし、$\overline{z}$ は $z$ の共役複素数とします。つまり、$z=x+iy$ のとき、
$\overline{z}=x-iy$ → $(x,-y)$ に対応
$-\overline{z}=-x+iy$ → $(-x,y)$ に対応
$-z=-x-iy$ → $(-x,-y)$ に対応

実数条件、純虚数条件

$z$ が実数であることは、$z$ が複素数平面の実軸上にあることを意味します。つまり実軸に関して対称移動した点 $\overline{z}$ と一致することを意味します。

$z$ の実部が $0$ であることは、$z$ が複素数平面の虚軸上にあることを意味します。つまり虚軸に関して対称移動した点 $-\overline{z}$ と一致することを意味します。ただし、$z=0$ は純虚数には含めないことに注意してください。

複素数平面内の距離

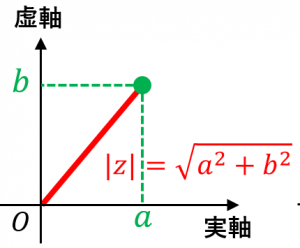
ただし、$|z|$ は複素数の絶対値を表します。つまり、$z=a+bi$ のとき、$|z|=\sqrt{a^2+b^2}$ です。

もっと詳しく：複素数の絶対値の意味と計算問題

複素数平面における円の方程式

極形式

実際、この複素数の実軸成分は $|z|\cos\theta$、虚軸成分は $|z|\sin\theta$ となり、それぞれ図の青い点線の長さと一致しています。

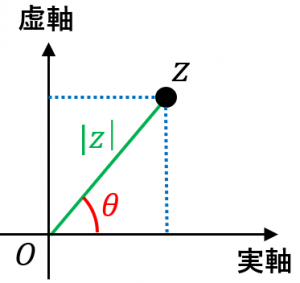
また、$\cos\theta+i\sin\theta$ のことは、$e^{i\theta}$ と書かれることもあります。
もっと詳しく：オイラーの公式e^πi=-1の意味と証明

また、偏角のことは、$\mathrm{arg}\:z$ と書くこともあります。
もっと詳しく：複素数の偏角の求め方と公式

複素数平面におけるかけ算

例えば、左側の図のような２つの複素数 $z_1,z_2$ に対して、積 $z_1z_2$ は右側の図のようになります。絶対値は $3\times 2=6$ で、偏角は $45^{\circ}+30^{\circ}=75^{\circ}$ となります。

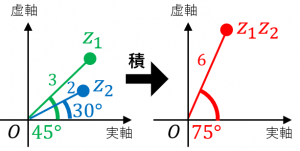
複素数平面におけるわり算

例えば、左側の図のような２つの複素数 $z_1,z_2$ に対して、商 $\dfrac{z_1}{z_2}$ は右側の図のようになります。絶対値は $3\div 2=1.5$ で、偏角は $45^{\circ}-30^{\circ}=15^{\circ}$ となります。

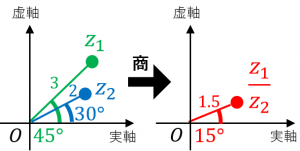
ド・モアブルの定理

$\cos\theta+i\sin\theta$ という複素数は、絶対値が $1$ で偏角が $\theta$ です。よって、これを $n$ 乗すると（公式13により）絶対値が $1$ で偏角が $n\theta$ の複素数になります。

15の関係式をド・モアブルの定理と呼びます。

1のn乗根

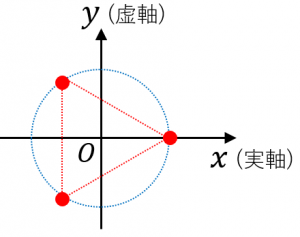
例えば、この公式で $n=3$ とすると、$1$ の三乗根（に対応する複素数）は、
・単位円上にある
・偏角は $0^{\circ},120^{\circ},240^{\circ}$
であることが分かります。1の三乗根に対応する複素数３つで、正三角形を作っています。

次回は 三次方程式の解と係数の関係と頻出問題 を解説します。