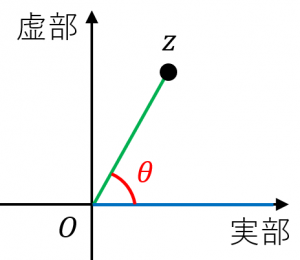
偏角とは、複素数 $z$ に対して、実軸の正の部分から、$z$ と原点を結ぶ線分までの角度 $\theta$ のことです。
このページでは、複素数平面における偏角について
・偏角とは何か?
・偏角に関する公式は?
といった疑問にお答えします。
偏角の求め方
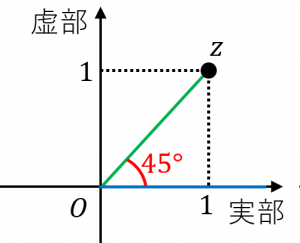
複素数平面で $1+i$ は、図の $z$ に対応します。このとき、図の $\theta$ は $45^{\circ}$ になるので、偏角は $45^{\circ}$ です。
複素数 $z$ の偏角を $\mathrm{arg}\:z$ と書くことが多いです。つまり、上記の結果を式で書くと、
$\mathrm{arg\:(1+i)}=45^{\circ}$
です。
分数の場合
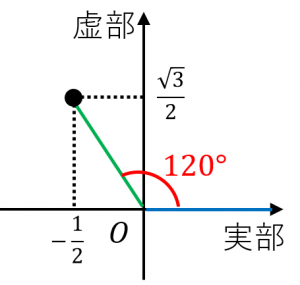
同じく図示してみましょう。偏角を $\theta$ とすると、$\tan$ の定義より、
$\tan\theta=\dfrac{\frac{\sqrt{3}}{2}}{-\frac{1}{2}}\\
=-\sqrt{3}$
になります。
$90^{\circ} < \theta < 180^{\circ}$ であることも考慮すると、$\theta=120^{\circ}$ であることが分かります。
(この記事では、偏角 $\theta$ は $0\leq\theta<360^{\circ}$ で表現することにします。)
$\tan\theta=\dfrac{b}{a}$ が成立します。
※つまり、偏角は実部と虚部の比だけで決まります。
※定数倍しても偏角は変わらないので、先に定数をかけて分母を払ってから偏角を求めることもできます。
偏角の公式
複素数 $z$ の絶対値を $r$、偏角を $\theta$ とおくと、
$z=r(\cos\theta+i\sin\theta)$
と表すことができます。この表し方を極形式と言います。
積の複素数の偏角は、偏角の和になります(→※):
$\mathrm{arg}\:(wz)=\mathrm{arg}\:w+\mathrm{arg}\:z$
商の複素数の偏角は、偏角の差になります(→※):
$\mathrm{arg}\:\left(\dfrac{w}{z}\right)=\mathrm{arg}\:w-\mathrm{arg}\:z$
※このページでは、偏角 $\theta$ は $0\leq\theta<2\pi$ を満たすようなもの(主値)で表現しました。そのため、積の複素数の偏角の公式は、厳密には、
$\mathrm{arg}\:(wz)\equiv\mathrm{arg}\:w+\mathrm{arg}\:z\:\mod 2\pi$
が正しい式です。同様に、商の公式は
$\mathrm{arg}\:\left(\dfrac{w}{z}\right)\equiv\mathrm{arg}\:w-\mathrm{arg}\:z\:\mod 2\pi$
が正しい式です。
次回は 複素数平面について、定義から難しい公式まで16個の知識 を解説します。
