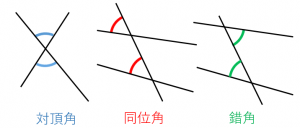
左側の図のように「互いに向かい合う」2つの角を対頂角と言います。
まん中の図のように「同じ位置にある」2つの角を同位角と言います。
右側の図のような2つの角を錯角と言います。
対頂角とは
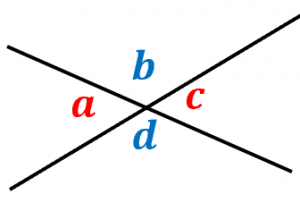
$\angle a$ と $\angle c$ は対頂角です。
$\angle b$ と $\angle d$ は対頂角です。
対頂角は必ず等しくなります。例えば、$\angle a=50^{\circ}$ の場合、$\angle c=50^{\circ}$ になります。
同位角と平行線
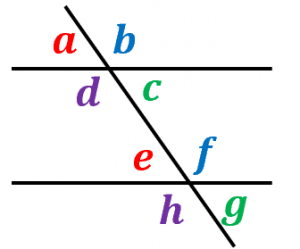
$\angle a$ と $\angle e$ は同位角
$\angle b$ と $\angle f$ は同位角
$\angle c$ と $\angle g$ は同位角
$\angle d$ と $\angle h$ は同位角
となります。
また、「異なる2本の直線」が平行な場合、同位角は等しくなります。例えば $\angle a= 60^{\circ}$ の場合、 $\angle e=60^{\circ}$ になります。
さらに、対頂角が等しいことも考えると、
$\angle c=\angle g=60^{\circ}$
になります。
「平行なら同位角が等しい」と覚えましょう。逆に、同位角が1ペアでも等しければ、「異なる2本の直線」は平行になります。よって、残りの3ペアの同位角も全て等しくなります。
錯角と平行線
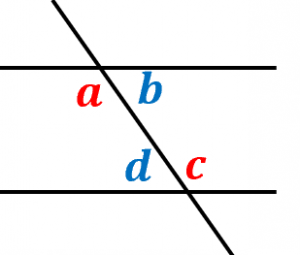
$\angle a$ と $\angle c$ は錯角
$\angle b$ と $\angle d$ は錯角
となります。
錯角は「同位角の対頂角(内側ペア)」と言うこともできます。
また、「異なる2本の直線」が平行な場合、錯角は等しくなります。例えば、$\angle a=130^{\circ}$ の場合、$\angle c=130^{\circ}$ になります。
「平行なら錯角が等しい」と覚えましょう。逆に、錯角が1ペアでも等しければ、「異なる2本の直線」は平行になります。よって、残りの1ペアの錯角も等しくなります。
錯角は特に重要
1. 対頂角は等しい
2. 平行線の同位角は等しい
3. 平行線の錯角は等しい
特に、3の錯角は、中学数学や高校数学でもいろいろな応用があります。
・四角形の内角の和が360度であることの証明に錯角が使えます。
四角形の内角の和が360°であることの2通りの証明
・平行四辺形の性質の証明に錯角を使います。
平行四辺形の3つの性質とその証明
・角の二等分線定理の証明に錯角を使います。
角の二等分線定理(内角、外角それぞれ)
・錯角を使って相似な三角形を見つけることができます。
三角形の相似条件と有名な例題3問
