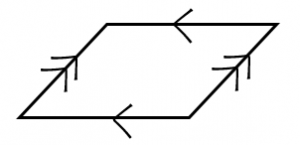
2組の対辺がそれぞれ平行な四角形を平行四辺形と言う。平行四辺形には、
・向かい合う辺の長さが等しい
・向かい合う角の大きさが等しい
・対角線が互いに中点で交わる
という3つの重要な性質がある。
1.向かい合う辺の長さが等しい
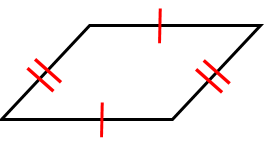
性質1:平行四辺形の2組の向かい合う辺の長さはそれぞれ等しい
三角形の合同を用いてこれを証明してみましょう。
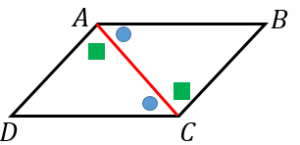
図のように平行四辺形に対角線 $AC$ を引きます。すると、
・平行線の錯角は等しいので $\angle BAC=\angle DCA$
・平行線の錯角は等しいので $\angle BCA=\angle DAC$
・$AC$ は共通
となり、1辺とその両端の角がそれぞれ等しいので三角形 $ABC$ と $CDA$ は合同になります。
よって、$AB=CD$、$BC=DA$ が分かります。
2.向かい合う角の大きさが等しい
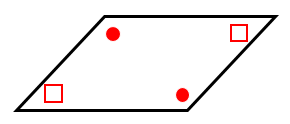
性質2:平行四辺形の2組の向かい合う角の大きさはそれぞれ等しい
これは、性質1で証明した結果を使えば簡単に証明できます。

さきほどと同様に平行四辺形に対角線 $AC$ を引きます。すると、三角形 $ABC$ と $CDA$ は合同でした。よって、$\angle B=\angle D$ が分かります。
同様に(対角線 $BD$ を引くと三角形 $ABD$ と $CDB$ は合同になるので)$\angle A=\angle C$ も分かります。
3.対角線が互いに中点で交わる
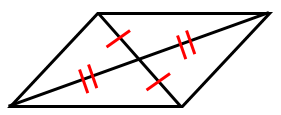
性質3:平行四辺形の2本の対角線はそれぞれの中点で交わる
今度は別の三角形の合同を使って性質3を証明します。
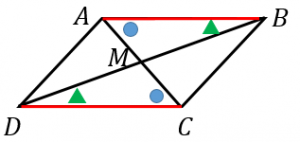
図のように、対角線の交点を $M$ とします。すると、
・平行線の錯角は等しいので $\angle MAB=\angle MCD$
・平行線の錯角は等しいので $\angle MBA=\angle MDC$
・性質1より $AB=CD$
となり、1辺とその両端の角がそれぞれ等しいので三角形 $ABM$ と $CDM$ は合同になります。
よって、$MA=MC$、$MB=MD$ となり、2本の対角線は互いの中点で交わることが分かります。
平行四辺形が非常に対称性の高いきれいな四角形であることが分かりました。ちなみに、もっと「きれいな」四角形として、長方形、ひし形、正方形があります。
参考:平行四辺形、ひし形、長方形、正方形の違い
次回は 対称の軸・線対称の意味と、正多角形などでの本数 を解説します。
