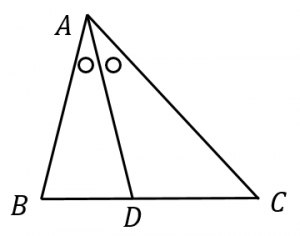
角の二等分線定理(内角バージョン)
図において、$AB:AC=BD:CD$
角の二等分線定理について、証明と応用例を解説します。
定理の証明
$C$ を通り $AB$ と平行な直線と $AD$ の交点を $E$ とします。
三角形 $ABD$ と $ECD$ は相似なので、
$AB:CE=BD:CD$
が成立します。
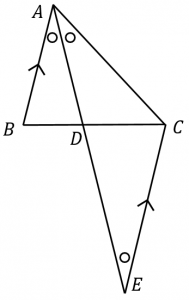
一方、平行線の錯角は等しいので $\angle BAD=\angle AEC$ です。よって、$\angle AEC=\angle EAC$ なので、$AC=CE$ となります。
以上2つの式から、$AB:AC=BD:CD$ が分かります。
余談(高校生向け):少し難しいですが、三角比を知っている人は以下のようにもっと簡単に証明できます:
$BD:DC\\
=|ABD|:|ACD|\\
=AB\cdot AD\cdot\sin \angle BAD\\
:AC\cdot AD\cdot\sin\angle CAD\\
=AB:AC$
(ただし、$|ABD|$ は三角形 $ABD$ の面積を表します)
応用例

例題:三角形 $ABC$ において、$AB=4$、$AC=5$、$BC=6$ である。$\angle A$ の二等分線と $BC$ の交点を $D$ とする。このとき、辺の長さの比 $BD:CD$ を求めよ。また、$BD$ の長さを求めよ。
解答:
角の二等分線定理より、$AB:AC=BD:CD$
よって、$BD:CD=4:5$
これを使うことで $BD$ の長さを計算することができます:
$BD=BC\times \dfrac{4}{4+5}\\
=\dfrac{4}{9}BC\\
=\dfrac{4}{9}\times 6\\
=\dfrac{8}{3}$
この問題をさらに発展させた有名な問題として、三角形の内心の証明と頻出例題2問の例題2があります。
外角バージョンとその証明
外角の二等分線についても同様に辺の比に関する定理が成立します。
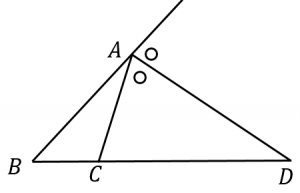
つまり、図において $AB:AC=BD:CD$ が成立します。
証明の流れも内角バージョンの場合と同じです。
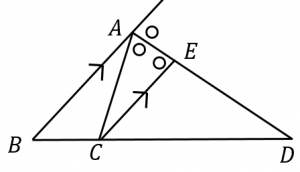
$C$ を通り $AB$ と平行な直線と $AD$ の交点を $E$ とすると、
$AB:CE=BD:CD$
が成立します。
一方、平行線の錯角は等しいことを使うと、$\angle AEC=\angle EAC$ が分かり、$AC=CE$ となります。
以上2つの式から、$AB:AC=BD:CD$ が分かります。
次回は 二等辺三角形の底角が等しいことの証明など を解説します。
