実数の意味と例（0、負の数、…）および実数でないものの例

実数の分類と例

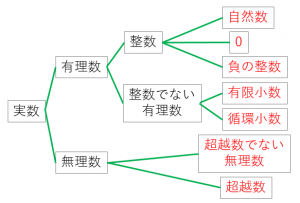
・自然数
$1,2,3,\cdots$

・$0$
0も実数です！

・負の整数
$-1,-2,-3,\cdots$ などの負の数も実数です！

・有限小数：$0.3, -0.24555$ など

・循環小数：$0.23232323\cdots$ など
有限小数と循環小数を合わせて有理数と呼びます。有理数とは分母と分子が両方整数であるような分数と言うこともできます。
関連：有理数と無理数の意味といろいろな例

・超越数でない無理数：$\sqrt{2},\sqrt{3}$ など
有限小数でも循環小数でも表せない実数のことを無理数と言います。無理数はさらに「超越数」「超越数でないもの」に分類されます。

・超越数：円周率 $\pi$、自然対数の底 $e$ など
関連：ネイピア数（自然対数の底）の意味と、重要である理由

実数でないものの例

・虚数
例えば、高校数学では虚数というものを習います。具体的には、$i^2=-1$ を満たすような $i$ について考えます。二乗してマイナスになる数は実数の範囲では存在しないので、$i$ は実数ではありません。

また、$3i$、$2-5i$ なども虚数となります。

ちなみに、実数と虚数を合わせて複素数と呼びます。「実数とは、複素数の中で虚数でないもの」と言うこともできます。

・四元数
複素数をさらに拡張した四元数というものもあります。
複素数は $a+bi$（$a,b$ は実数）という形の数でしたが、四元数は $a+bi+cj+dk$（$a,b,c,d$ は実数）という形の数です。

補足、まめ知識

・実数をきちんと定義（構成）するのは実はけっこう大変です。大学数学のレベルになります。

・実数全体の集合を表す記号として、$\mathbb{R}$ を用いることがあります。これは「実数」の英語「Real Number」の頭文字が R だからです。

次回は 式の展開（やり方、公式、ツール） を解説します。