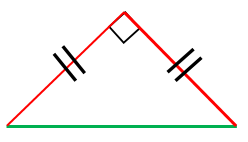
直角二等辺三角形の辺の長さの求め方

直角二等辺三角形とは

「直角三角形」かつ「二等辺三角形」である三角形を直角二等辺三角形と言います。直角二等辺三角形の内角はそれぞれ $45^{\circ}$、$45^{\circ}$、$90^{\circ}$ となります。
関連：二等辺三角形の底角が等しいことの証明など

直角二等辺三角形の最も長い辺のことを斜辺と呼びます。斜辺以外の辺を他の辺と呼ぶことにします。

斜辺の長さを求める

例題１

図のように斜辺でない辺の長さが $3\:\mathrm{cm}$ である直角二等辺三角形において、斜辺の長さを求めよ。

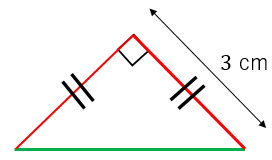
きちんとした値を求める（中学数学）

他の辺の長さを $\sqrt{2}$ 倍すれば斜辺の長さになるので、答えは
$3\times\sqrt{2}=3\sqrt{2}\:\mathrm{cm}$
です。

おおよその値を求める（算数）

きちんとした答えにはルートが入るので、算数しか知らない小学生に説明するときは、
他の辺の長さを $1.4$ 倍すればだいたい斜辺の長さになると言うとよいでしょう。
例題１の場合、答えはおおよそ $3\times 1.4=4.2\:\mathrm{cm}$ となります。

他の辺の長さを求める

例題２

図のように斜辺の長さが $5\:\mathrm{cm}$ である直角二等辺三角形において、$AB$ の長さを求めよ。

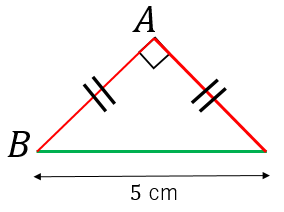
斜辺の長さを $\sqrt{2}$ で割れば他の辺の長さになるので、答えは
$5\div\sqrt{2}=\dfrac{5}{\sqrt{2}}=\dfrac{5}{2}\sqrt{2}\:\mathrm{cm}$
です。
関連：分母の有理化：m/√nの形

こちらも同様に、小学生に説明するときは、
斜辺の長さを $1.4$ で割ればだいたい他の辺の長さになると言うとよいでしょう。

公式が成り立つ理由

(斜辺の長さ) = $\sqrt{2}\times$ (他の辺の長さ)
を証明してみましょう。中学数学で習う三平方の定理を使います。

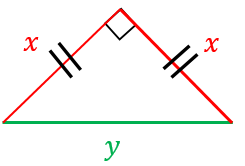
他の辺の長さを $x$、斜辺の長さを $y$ とすると、三平方の定理より、
$x^2+x^2=y^2$
です。

つまり、$2x^2=y^2$ です。
この両辺のルートを取ると、$\sqrt{2}x=y$ となります。

つまり、斜辺の長さは他の辺の長さの $\sqrt{2}$ 倍です！

次回は 直角三角形の辺の長さの求め方と計算ツール を解説します。