直角三角形の辺の長さの求め方と計算ツール

直角三角形で２つの辺の長さが分かっているときに、もう１つの辺の長さを求める方法を説明します。

長い辺（斜辺）を求める方法

直角三角形の直角をはさむ２つの辺の長さを $a$、$b$ として、長い辺の長さを $c$ とします。

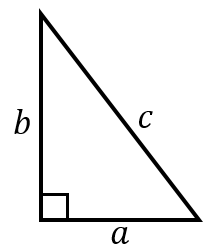
このとき、
$a\times a+b\times b=c\times c$
が成立します。これを三平方の定理、またはピタゴラスの定理と言います。

長い辺の長さを $c$ とすると、
$2\times 2+3\times 3=c\times c$
となります。計算すると、
$4+9=c\times c$
$13=c\times c$

よって、長い辺の長さは $c=\sqrt{13}$（二乗して $13$ になる正の数）となります。

では、$\sqrt{13}$ はどれくらいの長さでしょうか？
$3\times 3=9$
$c\times c=13$
$4\times 4=16$
なので、$\sqrt{13}$ は $3$ より大きくて $4$ より小さい数だと分かります。もう少しきちんと計算すると、
$\sqrt{13}=3.605551\cdots$
となります。

計算ツール

斜辺の長さを求めたいときに使ってください。

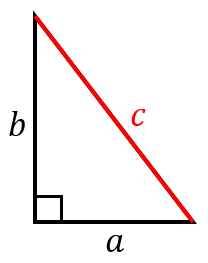
ちなみに、$a=3$、$b=4$ とすると、$c=5$ となります。全てが整数になるのは面白いですね。
→直角三角形で、3辺の比が整数になる例25個と作り方

短い辺の長さを求める方法

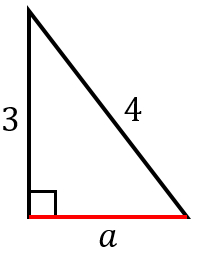
下側の辺の長さを $a$ とすると、
$a\times a+3\times 3=4\times 4$
となります。計算すると、
$a\times a+9=16$
$a\times a=16-9=7$

よって、下側の長さは $c=\sqrt{7}$ となります。きちんと計算すると、
$\sqrt{7}=2.645751\cdots$
となります。

関連：ルート2、ルート3、ルート5…ルート30の値と語呂合わせ

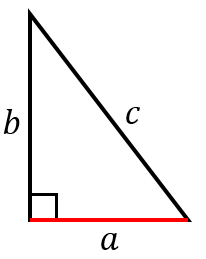
計算ツール

次回は 平行四辺形の3つの性質とその証明 を解説します。