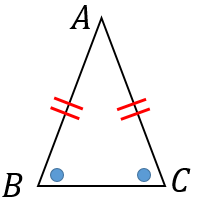
1:$AB=AC$ である二等辺三角形について、2つの底角は等しい。
2:逆に、2つの底角が等しいならば二等辺三角形である。
二等辺三角形について、重要な性質とその証明を解説します。
1(底角が等しいこと)の証明
二等辺三角形なら底角が等しいを証明します。
つまり、$AB=AC$ のとき、$\angle B=\angle C$ であることを証明します。
証明
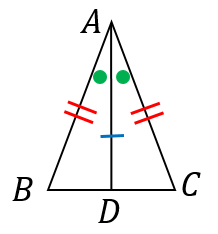
まず、$\angle A$ の二等分線を引き、$BC$ との交点を $D$ とおきます。
すると、2辺とその間の角がそれぞれ等しい(→補足)ので、三角形 $ABD$ と $ACD$ は合同になります。よって、$\angle B=\angle C$ となります。
補足
・仮定より $AB=AC$
・$AD$ は共通の辺
・角の二等分線なので $\angle BAD=\angle CAD$
2(二等辺三角形であること)の証明
底角が等しいなら二等辺三角形を証明します。
つまり、$\angle B=\angle C$ のとき、$AB=AC$ であることを証明します。
証明
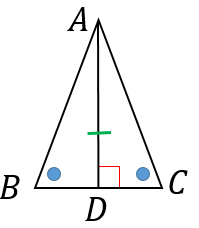
まず、$A$ を通り $BC$ に垂直な直線と $BC$ の交点を $D$ とします。
すると、1辺とその両端の角がそれぞれ等しい(→補足)ので、三角形 $ABD$ と $ACD$ は合同になります。よって、$AB=AC$ となります。
補足
・$AD$ は共通
・$\angle ADB=\angle ADC=90^{\circ}$
・$\angle BAD=\angle CAD$(三角形 $ABD$ と $ACD$ について、残りの2つの内角が等しいことので、3つの内角全てが等しいと分かる)
二等辺三角形の他の性質
先ほどの証明の図について、三角形 $ABD$ と $ACD$ は合同だったので、$BD=DC$ であることが分かります。
つまり、二等辺三角形において、底辺の垂直二等分線は $A$ を通ることが分かります。
また、二等辺三角形において、頂角 $A$ の二等分線は $BC$ の中点を通ると言うこともできます。
これらの性質は二等辺三角形が関わる問題で重要になることが多いので、ぜひとも覚えておきましょう。
関連:二等辺三角形の4つの性質と4つの条件
次回は 鋭角三角形と鈍角三角形の意味と見分け方 を解説します。
