直角三角形で、3辺の比が整数になるようなもの(ピタゴラス数)について、25個の例と作り方を紹介します。
長さが全て整数の直角三角形
直角三角形で、3つの辺の長さが全て整数になる場合はどのような場合でしょうか?
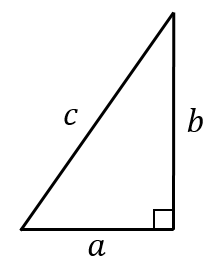
実は、3つの辺の長さを $a$、$b$、$c$ とすると、
直角三角形になる $\iff$ $a^2+b^2=c^2$
となることが知られています。
(中学数学で習うピタゴラスの定理から分かります)
例えば、$3^2+4^2=5^2$
($9+16=25$ ですね)
なので、$3:4:5$ の直角三角形が存在します!
このような $a,b,c$ の組をピタゴラス数と言います。ピタゴラス数を $25$ 組挙げてみます。
ピタゴラス数25個
$a,b,c$
$3,4,5$(とても有名)
$5,12,13$(有名)
$7,24,25$(少し有名)
$9,40,41$
$11,60,61$
$13,84,85$
$15,8,17$(少し有名)
$15,112,113$
$17,144,145$
$19,180,181$
$21,20,29$
$27,36,45$
$33,56,65$
$35,12,37$
$39,80,89$
$45,28,53$
$45,108,117$
$51,140,149$
$55,48,73$
$63,16,65$
$65,72,97$
$75,100,125$
$77,36,85$
$91,60,109$
$99,20,101$
作り方
次に、ピタゴラス数の作り方を説明します。
実は、$m$ を適当な奇数、$n$ を適当な偶数として、
$a=|m^2-n^2|$、$b=2mn$、$c=m^2+n^2$
とすれば、ピタゴラス数が得られます。
例えば $m=1$, $n=2$ とすると、
$a=|1^2-2^2|=3$、
$b=2\times 1\times 2=4$、
$c=1^2+2^2=5$
となり、$3:4:5$ という有名なピタゴラス数が得られます。
また、試しに、$m=9$、$n=4$ とすると、
$a=|81-16|=65$、
$b=2\times 9\times 4=72$、
$c=81+16=97$
となり、$65:72:97$ という巨大なピタゴラス数が得られます。
このような方法でピタゴラス数がたくさん作れるのは、
$|m^2-n^2|^2+(2mn)^2=(m^2+n^2)^2$
という等式が成立するからです。
ちなみに、$m$ を奇数、$n$ を偶数としたのは、$a,b,c$ が全て偶数になるのを防ぐためです。(全部偶数だと全部 $2$ で割ることで、もっとシンプルなピタゴラス数を得ることができるので、あまりおもしろくありません)
次回は 反比例の意味と身近な例4つ を解説します。
