(ひし形、正方形など)対角線が直交する四角形なら、
(面積)=(対角線)×(対角線)×$\dfrac{1}{2}$
公式を使う例と説明
例題1:図のような四角形の面積を求めよ。
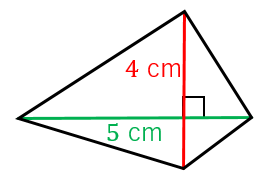
対角線が直角に交わる場合には、対角線の長さをかけ算して $2$ で割れば面積を求めることができます。この場合、面積は
$4\times 5\div 2=10\:\mathrm{cm}^{2}$
となります。
では、この公式が成り立つ理由を説明します。
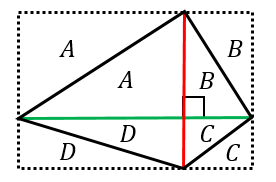
(対角線)×(対角線)は
(大きな長方形の横)×(大きな長方形の縦)=長方形の面積と一致します。つまり $2A+2B+2C+2D$
になります。これを $2$ で割ると、$A+B+C+D$ となり、求めたい四角形の面積になります。
一般の四角形では?
上の公式は対角線が直交する四角形にしか使えません(長方形や台形でも使えないです)。対角線が直交しない場合はどうすればよいでしょうか?
実は、対角線が直角に交わらない場合でも、対角線の長さと面積の間には関係があります。ただし、高校数学で習う三角比の考え方が必要です。
どんな四角形でも、対角線のなす角を $\theta$ とおくと、
(面積)=(対角線)×(対角線)×$\dfrac{1}{2}\times\sin\theta$
が成立します。
例題2:図のような等脚台形の面積を計算せよ。
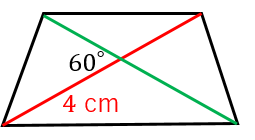
等脚台形の対角線の長さは等しいので、面積は、
$4\times 4\times \dfrac{1}{2}\times \sin 60^{\circ}\\
=8\times \dfrac{\sqrt{3}}{2}\\
=4\sqrt{3}$
一般の場合の公式の証明
(面積)=(対角線)×(対角線)×$\dfrac{1}{2}\times\sin\theta$
を証明します。
図のように、対角線の交点から各頂点までの距離を $a,\:b,\:c,\:d$ とおきます。
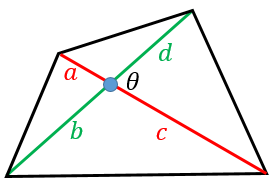
左側の三角形の面積は、
$\dfrac{1}{2}ab\sin\theta$
下側の三角形の面積は、
$\dfrac{1}{2}bc\sin(180^{\circ}-\theta)\\
=\dfrac{1}{2}bc\sin\theta$
よって、この2つを足すと
$\dfrac{1}{2}b(a+c)\sin\theta$
となります。
同様に、右側と上側の三角形の面積の和は、
$\dfrac{1}{2}cd\sin\theta+\dfrac{1}{2}da\sin(180^{\circ}-\theta)\\
=\dfrac{1}{2}cd\sin\theta+\dfrac{1}{2}ad\sin\theta\\
=\dfrac{1}{2}d(a+c)\sin\theta$
よって、4つの三角形の面積の和は、
$\dfrac{1}{2}(a+c)(b+d)\sin\theta$
となります。
$(a+c)$ と $(b+d)$ はもとの四角形の対角線の長さなので、公式が証明できました。
次回は 正六角形の面積(計算ツール、公式の導出) を解説します。
