正六角形の面積公式
~近似値を求めたい人、小学生向け~
(一辺)×(一辺)×$2.6$
~厳密な値を求めたい人、高校生向け~
$\dfrac{3\sqrt{3}}{2}a^2$($a$ は一辺の長さ)
面積計算ツール
例題
一辺の長さが $2\:\mathrm{cm}$ である正六角形の面積を求めよ。
答え:公式より、$\dfrac{3}{2}\sqrt{3}\cdot 2^2=6\sqrt{3}\:\mathrm{cm}^2$
公式の証明(中学生以上向け)
一辺が $a$ の正三角形の面積が $\dfrac{\sqrt{3}}{4}a^2$ であることを使います。ご存じでない方は正三角形の面積の求め方(小学生用~高校生用)を御覧ください。
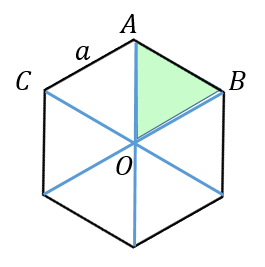
正六角形の内角の和は $180(6-2)=720^{\circ}$ です。なので、$\angle CAB=720\div 6=120^{\circ}$ です。
よって、$\angle OAB$ はその半分の $60^{\circ}$ です。
同様に、$\angle OBA=60^{\circ}$ です。
よって、三角形 $OAB$ は全ての内角が $60^{\circ}$ なので正三角形となります。正六角形はこのサイズの正三角形 $6$ 個ぶんなので面積は、
$\dfrac{\sqrt{3}}{4}a^2\times 6=\dfrac{3}{2}\sqrt{3}a^2$
となります。
小学生でも分かる公式
きちんとした値には $\sqrt{3}$ が入ってくるので、小学校の算数の範囲内で計算することはできません。ですが、おおよその値なら計算することができます。
$\tfrac{3}{2}\sqrt{3}\simeq 2.598$ なので、正六角形の面積は(おおよそ)、
(一辺の長さ)×(一辺の長さ)×$2.6$
となります。
次回は 多角形の対角線の本数を求める公式 を解説します。
