多角形の対角線の本数を求める公式

多角形の対角線の本数を求める公式について、具体例と公式が成り立つ理由を解説します。

対角線の本数を計算する具体例

公式：$\dfrac{1}{2}n(n-3)$
で $n=4$ とすると、
$\dfrac{1}{2}\times 4\times(4-3)=2$ 本
であることが分かります。

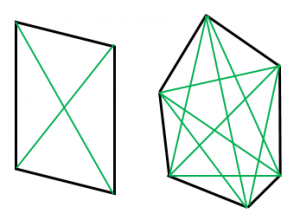
公式：$\dfrac{1}{2}n(n-3)$
で $n=6$ とすると、
$\dfrac{1}{2}\times 6\times(6-3)=9$ 本
であることが分かります。
（実際に9本あることを図で確認してみてください！）

図を書かなくても対角線の本数が計算できる

公式：$\dfrac{1}{2}n(n-3)$
で $n=8$ とすると、
$\dfrac{1}{2}\times 8\times(8-3)=20$ 本
であることが分かります。

※四角形や六角形なら図をかいて数えればよいですが、八角形などとなると、公式を使わないと大変です。

公式が成り立つ理由

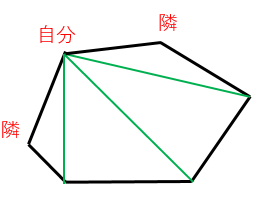
特定の頂点から対角線は $(n-3)$ 本引けます（自分と自分の隣以外の頂点は $(n-3)$ 個だから）。頂点は、$n$ 個あるので、のべ $n(n-3)$ 本の対角線を考えることができます。

ただし、これだと一本の対角線は2回カウントされてしまうので、これを $2$ で割ったものが対角線の本数になります：
$n(n-3)\div 2=\dfrac{1}{2}n(n-3)$

余談：上記のような組合せの考え方ではなく、高校数学で学ぶ漸化式というものを使って証明することもできます。

対角線の本数から何角形か求める

例えば、多角形の対角線の本数が $35$ 本であったとき、この多角形は何角形か計算してみましょう。

対角線の本数：$\dfrac{1}{2}n(n-3)$ が $35$ と等しいので、
$\dfrac{1}{2}n(n-3)=35$

です。これを整理すると、
$n(n-3)=70$
$n^2-3n-70=0$
$(n-10)(n+7)=0$
$n=10,-7$
→二次方程式の例題４問

ここで、$n$ は正なので、$n=10$ です。つまり、答えは十角形ということになります。

次回は 正弦定理を使う例題2問と証明 を解説します。