数学Iで学ぶ三角比の公式を一覧にしました。
数学Iの三角比では、
三角比の定義
有名角の値
三角比の相互関係
捕角・余角の公式
正弦定理・余弦定理
の5つをしっかり覚えればOKです。(数学IIの三角関数では、これらに加えて加法定理を覚える必要があります)
三角比の定義
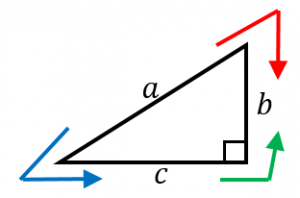
・$\sin\theta=\dfrac{b}{a}$
・$\cos\theta=\dfrac{c}{a}$
・$\tan\theta=\dfrac{b}{c}$
関連:単位円を使った三角比の定義と有名角の値(0°~180°)
有名角の値
$\sin 30^{\circ}=\dfrac{1}{2}$、$\cos 30^{\circ}=\dfrac{\sqrt{3}}{2}$、$\tan 30^{\circ}=\dfrac{1}{\sqrt{3}}$
$\sin 45^{\circ}=\dfrac{1}{\sqrt{2}}$、$\cos 45^{\circ}=\dfrac{1}{\sqrt{2}}$、$\tan 45^{\circ}=1$
$\sin 60^{\circ}=\dfrac{\sqrt{3}}{2}$、$\cos 60^{\circ}=\dfrac{1}{2}$、$\tan 60^{\circ}=\sqrt{3}$
相互関係
・$\tan\theta=\dfrac{\sin\theta}{\cos\theta}$
・$\sin^2\theta+\cos^2\theta=1$
・$1+\tan^2\theta=\dfrac{1}{\cos^2\theta}$
捕角・余角の公式
・$\sin(180^{\circ}-\theta)=\sin\theta$
・$\cos(180^{\circ}-\theta)=-\cos\theta$
・$\tan(180^{\circ}-\theta)=-\tan\theta$
・$\sin(90^{\circ}-\theta)=\cos\theta$
・$\cos(90^{\circ}-\theta)=\sin\theta$
・$\tan(90^{\circ}-\theta)=\dfrac{1}{\tan\theta}$
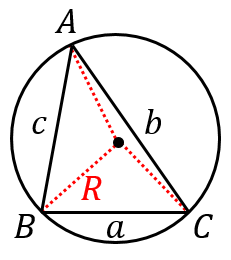
正弦定理、余弦定理
・正弦定理
$\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}=2R$
正弦定理を使う例題2問と証明
・余弦定理
$a^2=b^2+c^2-2bc\cos A$
$b^2=c^2+a^2-2ca\cos B$
$c^2=a^2+b^2-2ab\cos C$
余弦定理の証明と例題
次回は 30度、45度、60度のsin、cos、tan を解説します。
