$\sin 30^{\circ}=\dfrac{1}{2}$、$\cos 30^{\circ}=\dfrac{\sqrt{3}}{2}$、$\tan 30^{\circ}=\dfrac{1}{\sqrt{3}}$
$\sin 45^{\circ}=\dfrac{1}{\sqrt{2}}$、$\cos 45^{\circ}=\dfrac{1}{\sqrt{2}}$、$\tan 45^{\circ}=1$
$\sin 60^{\circ}=\dfrac{\sqrt{3}}{2}$、$\cos 60^{\circ}=\dfrac{1}{2}$、$\tan 60^{\circ}=\sqrt{3}$
30度、45度、60度の三角比の値と求め方を確認します。
30度の三角比
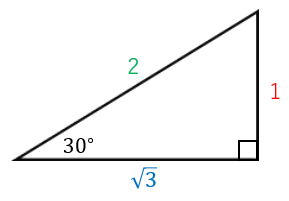
サインは (遠い辺)/(斜辺) なので、$\dfrac{1}{2}$ となります。
コサインは (近い辺)/(斜辺) なので、$\dfrac{\sqrt{3}}{2}$ となります。
タンジェントは (遠い辺)/(近い辺) なので、$\dfrac{1}{\sqrt{3}}$ となります。
45度の三角比
関連:直角二等辺三角形の辺の長さの求め方
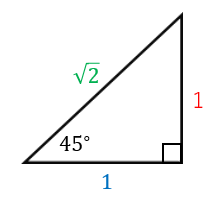
サインは (遠い辺)/(斜辺) なので、$\dfrac{1}{\sqrt{2}}$ となります。
コサインは (近い辺)/(斜辺) なので、$\dfrac{1}{\sqrt{2}}$ となります。
タンジェントは (遠い辺)/(近い辺) なので、$1$ となります。
60度の三角比
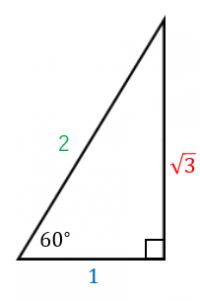
サインは (遠い辺)/(斜辺) なので、$\dfrac{\sqrt{3}}{2}$ となります。
コサインは (近い辺)/(斜辺) なので、$\dfrac{1}{2}$ となります。
タンジェントは (遠い辺)/(近い辺) なので、$\sqrt{3}$ となります。
まめ知識、補足
・30度と60度の三角比の間には
$\sin 30^{\circ}=\cos 60^{\circ}$、$\cos 30^{\circ}=\sin 60^{\circ}$、$\tan 30^{\circ}=\dfrac{1}{\tan 60^{\circ}}$
という関係があります。より一般に,$\sin \theta=\cos(90^{\circ}-\theta)$、$\tan\theta=\dfrac{1}{\tan(90^{\circ}-\theta)}$ という公式が成立します。
・15度や18度などの三角比も計算することができますが、30度や45度よりかなり大変です。
関連:sin15度、cos15度、tan15度の値と求め方
関連:cos72度、sin18度の2通りの求め方
次回は 単位円を使った三角比の定義と有名角の値(0°~180°) を解説します。
