余弦定理の証明と例題

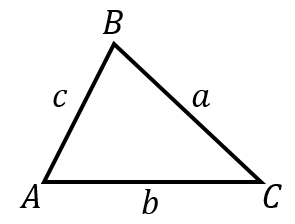
余弦定理の簡単な例題

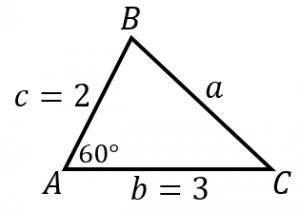
余弦定理：
$a^2=b^2+c^2-2bc\cos A$
に与えられた条件を代入すると、
$a^2=3^2+2^2-2\cdot 3\cdot 2\cdot\cos 60^{\circ}$
となります。$\cos 60^{\circ}=\dfrac{1}{2}$
なので、
$a^2=9+4-12\cdot\dfrac{1}{2}\\
=7$
となります。

よって、$a=\sqrt{7}$

６つの余弦定理

余弦定理は
$a^2=b^2+c^2-2bc\cos A$
を紹介しましたが、$a,b,c$ を入れ替えた以下の式も成立します：
$b^2=c^2+a^2-2ca\cos B$
$c^2=a^2+b^2-2ab\cos C$
（$A$、$B$、$C$ は内角　$a$、$b$、$c$ は辺の長さ）

さきほどの例題のように、余弦定理を使えば、二辺とその間の角度が分かっているときに、残りの一辺の長さを計算することができます。

さらに、余弦定理を $\cos$ について解くと、
$\cos A=\dfrac{b^2+c^2-a^2}{2bc}$
$\cos B=\dfrac{c^2+a^2-b^2}{2ca}$
$\cos C=\dfrac{a^2+b^2-c^2}{2ab}$
となります。これらのことも余弦定理と言うことがあります。

余弦定理の証明（鋭角の場合）

$\angle A$ が鋭角の場合に、
$a^2=b^2+c^2-2bc\cos A$
を証明してみましょう。
（鋭角の場合さえ理解できれば直角や鈍角も簡単です）

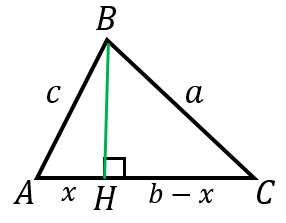
$AH=x$ とおくと、$CH=b-x$ です。
三角形 $ABH$ に三平方の定理を使うと、
$BH^2=c^2-x^2$
三角形 $BCH$ に三平方の定理を使うと、
$BH^2=a^2-(b-x)^2$

よって、
$c^2-x^2=a^2-(b-x)^2$
です。

これを整理すると、
$c^2-x^2=a^2-b^2-x^2+2bx$
$c^2=a^2-b^2+2bx$
$x=\dfrac{-a^2+b^2+c^2}{2b}$

また、$\cos$ の定義より、
$\cos A=\dfrac{AH}{BA}\\
=\dfrac{x}{c}
=\dfrac{b^2+c^2-a^2}{2bc}$

よって、
$2bc\cos A=b^2+c^2-a^2$
$a^2=b^2+c^2-2bc\cos A$

余弦定理の証明（直角、鈍角の場合）

$\angle A$ が直角の場合

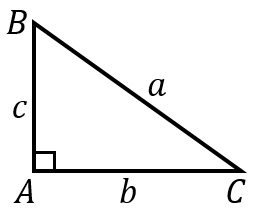
三平方の定理より、$a^2=b^2+c^2$ が成立します。
$\cos 90^{\circ}=0$ なので，$a^2=b^2+c^2$ という式は
$a^2=b^2+c^2-2bc\cos A$
と書いてもOKですね。
余弦定理は、直角三角形の場合には三平方の定理（ピタゴラスの定理）そのものというわけです。

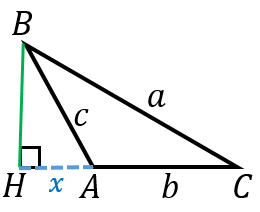
$\angle A$ が鈍角の場合

$AH=x$ とおくと、$CH=b+x$ です。
三角形 $ABH$ に三平方の定理を使うと、
$BH^2=c^2-x^2$
三角形 $BCH$ に三平方の定理を使うと、
$BH^2=a^2-(b+x)^2$

よって、
$c^2-x^2=a^2-(b^2+x^2+2bx)$
これを整理して $x$ について解くと、
$x=\dfrac{a^2-b^2-c^2}{2b}$

また、$\cos$ の定義より、
$\cos A\\
=\cos(180^{\circ}-\angle BAH)\\
=-\cos(\angle BAH)
=-\dfrac{AH}{BA}\\
=-\dfrac{x}{c}
=\dfrac{b^2+c^2-a^2}{2bc}$

よって、
$2bc\cos A=b^2+c^2-a^2$
$a^2=b^2+c^2-2bc\cos A$

次回は 三角比の公式一覧 を解説します。