最急降下法とは、最適化(関数の最小化または最大化)の有名な手法の一つです。
「今いる位置の近くだけを見て、一番良さそうな方向に進む」ことを繰り返す方法です。
最急降下法について例題を使って詳しく解説します。また、最急降下法の注意点、機械学習における使われ方についても述べます。
最急降下法の概要
1. 適当に初期点を選ぶ
2. 今いる位置における最急降下方向(関数の値が最も小さくなる方向)を計算する
最急降下方向は各変数での微分係数を並べたベクトル(勾配ベクトル)の反対向きです。具体的な計算方法は後述の例題参照。
関連:grad、div、rotの定義と意味
3. 最急降下方向に進む
移動距離(ステップ幅)をどうやって決めるのかも考える必要があります。
4. 2 と 3を繰り返す
収束したら(「これ以上移動しても関数の値がほとんど小さくならない」となったら)反復を終了します。
最急降下法の例題
$f(x,y)=x^2+y^2+xy-2x$ の最小化問題を最急降下法で解いてみる。
1. 適当に初期点を選ぶ
$(x_0,y_0)=(1,1)$ を初期点にしてみましょう。
2. 最急降下方向を計算する
$f(x,y)$ を $x$ で偏微分すると、$2x+y-2$
$f(x,y)$ を $y$ で偏微分すると、$2y+x$
よって、$(x_0,y_0)=(1,1)$ における最急降下方向は、$(1,3)$ の反対の向き。
つまり、$(-1,-3)$ の向き。
3. ステップ幅を決めて最急降下方向に進む
ステップ幅を $\alpha$ とおくと、移動後の点は
$(x_1,y_1)=(x_0,y_0)+\alpha(-1,-3)\\
=(1-\alpha,1-3\alpha)$
です。そこで、適切なステップ幅を求めるために $f(1-\alpha,1-3\alpha)$ を最小にするような $\alpha$ を計算すると、$\alpha=\dfrac{5}{13}$ となります(→補足)。
よって、$(x_1,y_1)=\left(\dfrac{8}{13},-\dfrac{2}{13}\right)$ です。初期点より最適解に近づいています。
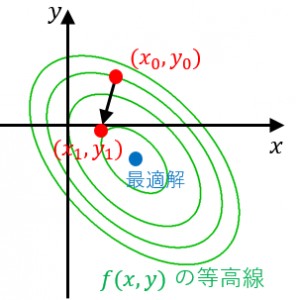
4. 2 と 3 を繰り返す
以下、同様な計算を繰り返して、どんどんゴールに近づいていきます。
補足:
1変数の二次関数の最小化なので、平方完成を使えば簡単にできます。詳細は省略します。
最急降下法の注意点
最急降下方向で進む方向を決めるときには、勾配の情報を使います。つまり、今いる点の近傍の情報しか使いません。よって、
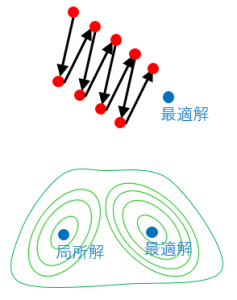
・たくさん反復しても思うようにゴールに近づかないことがあります(上側の図)。
・谷が複数ある場合、本当の最適解ではなく、局所解に収束してしまうことがあります(下側の図)。
また、先述の例ではステップ幅の計算は1変数の2次関数の最小化問題に帰着できたため、簡単にできましたが、一般には1変数関数の最小化でもそんなに綺麗には解けません。よって、ステップ幅の決め方も自分で考える必要があります。
機械学習における最急降下法
最急降下法は、多変数関数の最大化、最小化のための手法です。機械学習(特に、ニューラルネットワーク)では、誤差関数の最小化を行う機会が多く、最急降下法などのアルゴリズムが使われます。ニューラルネットワークの学習では、最急降下法をベースにしたアルゴリズムである確率的勾配降下法が使われることも多いです。
次回は 劣モジュラ関数最大化に対する貪欲アルゴリズム を解説します。
