確率的勾配降下法とは、勾配法という最適化手法において必要な勾配の計算を、確率を使うことで高速に行う方法です。
このページでは、確率的勾配降下法の意味を解説します。また、確率的勾配降下法を理解するために必要な前提として「普通の」勾配降下法についても説明します。
確率的勾配降下法とは
確率的勾配降下法とは、大雑把に言うと、
「勾配法」+「確率を使って勾配の計算を高速に行う」
ような最適化手法です。
つまり、確率的勾配降下法を理解するためには、
「(普通の)勾配法」
と
「確率を使って勾配の計算を高速に行う」
という2つの要素の理解が必要です。
それぞれについて解説します。
「普通の」勾配降下法
まずは、普通の勾配法(勾配降下法)について解説します。
勾配降下法では、以下の手順で最小化を行います。
(参考:最急降下法のイメージと例)
手順1.適当に初期点 $\overrightarrow{w}$ を選ぶ
手順2.今いる位置における最急降下方向(関数 $E$ の値が最も小さくなる方向)を計算する。
最急降下方向は、勾配ベクトルのマイナス1倍です。つまり $-\dfrac{\partial E(\overrightarrow{w})}{\partial\overrightarrow{w}}$ です。
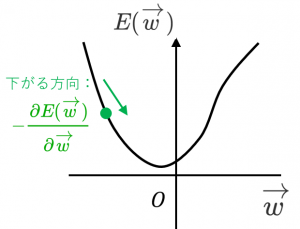
手順3.最急降下方向に進む
$\overrightarrow{w}\leftarrow\overrightarrow{w}-\eta\dfrac{\partial E(\overrightarrow{w})}{\partial\overrightarrow{w}}$
このとき、どれくらい移動するか(ステップ幅 $\eta$)を与える必要があります。
手順4.上記2と3を繰り返す
確率を使って勾配の計算を高速に行う
確率的勾配降下法の2つめの要素である「確率を使って勾配の計算を高速に行う」について説明します。
のように、和の形で書ける場合を考えてみます。
例えば、最小二乗法の文脈では、全体の誤差は
$E=\displaystyle\sum_{i=1}^n(f(x_i)-y_i)^2$
のように、各データの誤差の和で表されます。
(参考:最小二乗法と最尤法の関係)
この場合、データ数 $n$ が多くなると、$-\dfrac{\partial E(\overrightarrow{w})}{\partial\overrightarrow{w}}$ の計算が非常に大変です。
そこで、手順2と3で登場する $-\dfrac{\partial E(\overrightarrow{w})}{\partial\overrightarrow{w}}$ の変わりに $-\dfrac{\partial E_i(\overrightarrow{w})}{\partial\overrightarrow{w}}$ を使うのが、確率的勾配降下法(Stocastic Gradient Descent、SGD)です。$i$ は各反復で変えてやります。
例えば「全データ $1,\dots, n$ を確率的に(ランダムに)ソートし、順番に $E_i$ を使って $n$ 回反復していく」というのを何回か繰り返します。
関連する用語
・確率的勾配降下法のことをオンライン勾配降下法と言うことがあります。
(データ $i$ が到着するごとに、それに対応する誤差 $E_i$ を使ってパラメータの更新ができる → 逐次処理ができるというイメージです)
・それに対して「普通の」勾配降下法のことをバッチ勾配降下法と言うことがあります。
・オンライン勾配降下法とバッチ勾配降下法の中間を取った方法も考えられます。つまり、勾配の計算に、全データの誤差の和 $E$ でもなく、1つのデータの誤差 $E_i$ でもなく、いくつかのデータの誤差 $E_i$ の和を使う方法です。この方法を、ミニバッチ勾配降下法と言うことがあります。
| バッチ | ミニバッチ | オンライン | |
| 1回の反復の計算 | 全データを使うので計算が大変 | ほどほど | データ1つしか使わないので計算が楽 |
| 1回の反復の精度 | 全データを使うので良さそう | ほどほど | データを1つしか使わないので変な方向に進むことがある |
・確率的勾配降下法や、ミニバッチ勾配降下法において、全データを食わせる回数のことをエポック数と言うことがあります。例えば、データ数 $1000$ で、ミニバッチのサイズが $50$ のとき、$20$ 反復で全データを1周するので、$20$ 反復が1エポックに対応します。さらに、エポック数が $10$ なら、総反復回数は $200$ になります。
・ステップ幅 $\eta$ のことを学習率と言うことがあります。
次回は ロジット関数とロジスティック関数 を解説します。
