ベクトル解析の基本的な道具である grad、div、rot について説明します。
grad（勾配）の定義と例
ただし、$f$ は3変数 $(x,y,z)$ の関数とします。勾配は、それぞれの変数で偏微分したものを成分に持つベクトルです。各成分は、その方向に少し進んだときに関数 $f$ がどれくらい増えるかを表しています。
例えば、$f=x+y^2+z^3$ のとき、勾配ベクトルは $\mathrm{grad}\:f=(1,2y,3z^2)$ となります。
勾配ベクトルの $x$ 成分は、その点で $x$ 軸の向きに少し進んだときに $f$ がどれくらい増えるかを表します。$y$ 成分、$z$ 成分も同様です。
div（発散）の定義と例
ただし、$V=(V_x,V_y,V_z)$ はベクトル場とします。つまり、$V_x,V_y,V_z$ はそれぞれ $(x,y,z)$ の関数です。
発散は実数（スカラー）になります。
例えば、$V=(x+y+z,x^2+y^2+z^2,x^3+y^3+z^3)$ のとき、発散は
$\mathrm{div}\:V=1+2y+3z^2$
となります。
発散の意味（イメージ）
この解釈を説明します。一辺の長さが $\Delta x,\Delta y,\Delta z$ の直方体を考えます。
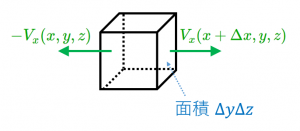
この直方体から $x$ 方向にあふれ出ている量は
$V_x(x+\Delta x,y,z)\Delta y\Delta z-V_x(x,y,z)\Delta y\Delta z\\
\fallingdotseq\dfrac{\partial V_x}{\partial x}\Delta x\Delta y\Delta z$
とみなせます。
同様に、$y$ 方向にあふれている量は
$\dfrac{\partial V_y}{\partial y}\Delta x\Delta y\Delta z$
で、$z$ 方向にあふれている量は
$\dfrac{\partial V_z}{\partial z}\Delta x\Delta y\Delta z$
とみなせます。
よって、この直方体からあふれている量は全部で
$\mathrm{div}\:V\Delta x\Delta y\Delta z$
とみなせます。これを体積 $\Delta x\Delta y\Delta z$ で割ると、単位体積あたりの量 $\mathrm{div}\:V$ が得られます。
rot（回転）の定義と例
ただし、$V=(V_x,V_y,V_z)$ はベクトル場とします。
回転はベクトルになります。
例えば、$V=(x+y+z,x^2+y^2+z^2,x^3+y^3+z^3)$ のとき、回転の $x$ 成分は
$\dfrac{\partial V_z}{\partial y}-\dfrac{\partial V_y}{\partial z}=3y^2-2z$
となります。$y$ 成分、$z$ 成分も同様に計算できます。
回転の意味（イメージ）
$x$ 成分、$y$ 成分も同様です。この解釈を簡単に説明します。
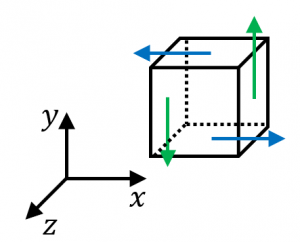
一辺の長さが $\Delta x,\Delta y,\Delta z$ の直方体を考えます。
緑の矢印と青い矢印が、$z$ 軸の正の向きにねじを回す力と考えられます。この「力」の大きさは
$V_y(x+\Delta x,y,z)\Delta y\Delta z-V_y(x,y,z)\Delta y\Delta z$
$-V_x(x,y+\Delta y,z)\Delta x\Delta z+V_x(x,y,z)\Delta x\Delta z$
$\fallingdotseq\dfrac{\partial V_y}{\partial x}\Delta x\Delta y\Delta z-\dfrac{\partial V_x}{\partial y}\Delta x\Delta y\Delta z$
とみなせます。
体積 $\Delta x\Delta y\Delta z$ で割ると、単位体積あたりの「ねじを回す力」が
$\dfrac{\partial V_y}{\partial x}-\dfrac{\partial V_x}{\partial y}$
であることが分かります。
次回は ナブラ演算子∇の4つの意味と計算公式 を解説します。
