二等辺三角形の4つの性質と4つの条件

二等辺三角形に関する用語

二等辺三角形に関して、底辺、底角、頂角という3つの言葉を覚えておきましょう。

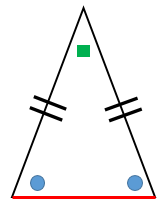
底辺とは、二等辺三角形で等しい2辺ではない残りの辺のことです。
底角とは、底辺に隣接する角のことです。底角は2つあります。
頂角とは、等しい2辺で挟まれた角のことです。

二等辺三角形の４つの性質

二等辺三角形の性質は４つあります。

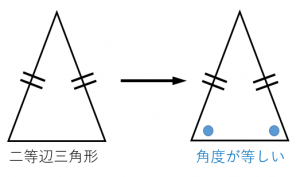
性質１：二等辺三角形の底角は等しい。

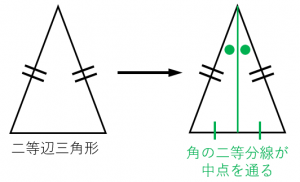
性質２：二等辺三角形の頂角の二等分線は底辺の中点を通る。

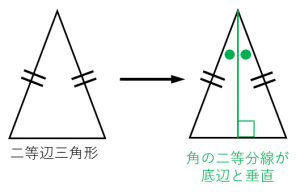
性質３：二等辺三角形の頂角の二等分線は底辺と直角に交わる。

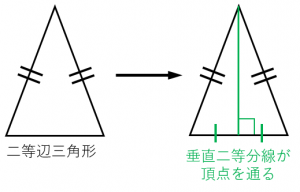
性質４：二等辺三角形の底辺の垂直二等分線は頂点を通る。

二等辺三角形になるための条件

三角形が以下の４つの条件のうち１つでも満たしていれば、それは二等辺三角形です。

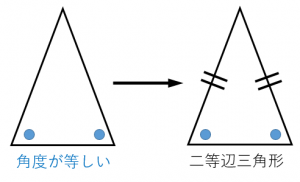
条件１：2つの角度が等しい三角形は二等辺三角形である。

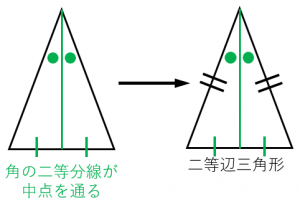
条件２：頂角の二等分線が底辺の中点を通る三角形は二等辺三角形である。

条件３：頂角の二等分線が底辺と垂直に交わる三角形は二等辺三角形である。

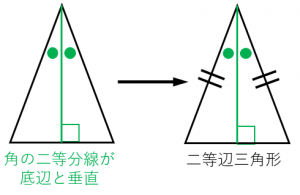
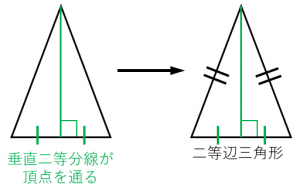
条件４：底辺の垂直二等分線が別の頂点を通る三角形は二等辺三角形である。

まとめ

二等辺三角形には
・底角が等しい
・頂角の二等分線が底辺の中点を通る
・頂角の二等分線が底辺と垂直に交わる
・底辺の垂直二等分線は別の頂点を通る
という４つの性質がありました。
逆に、上の4つのうちどれか1つでも成り立つ三角形は二等辺三角形となります。

次回は 二等辺三角形の角度の求め方と例題 を解説します。