二次関数のグラフとx軸の共有点の座標を求める

簡単な例題

$x$ 軸との共有点の $y$ 座標は $0$ なので、$x$ 座標は
$x^2-3x+2=0$ という二次方程式の解である。

これを因数分解すると、
$(x+1)(x+2)=0$
となり、解は $x=-1,-2$

よって、答えは $(-1,0)$ と $(-2,0)$

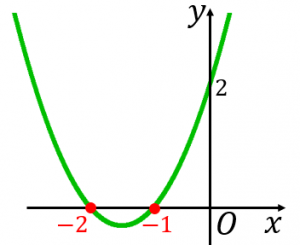
ちなみに、$y=x^2-3x+2$ のグラフは図のようになります。

関連：二次方程式の例題４問

解の公式を使う問題

$x$ 軸との共有点の $y$ 座標は $0$ なので、$x$ 座標は
$2x^2+5x-1=0$ という二次方程式の解である。

解の公式を使って解くと、
$x=\dfrac{-5\pm\sqrt{5^2-4\cdot 2\cdot(-1)}}{2\cdot 2}\\
=\dfrac{-5\pm\sqrt{33}}{4}$
となる。

よって、答えは $\left(\dfrac{-5+\sqrt{33}}{4},0\right)$ と $\left(\dfrac{-5-\sqrt{33}}{4},0\right)$

関連：二次方程式の解の公式と問題4問

共有点の個数

二次関数のグラフと $x$ 軸の共有点の個数を求めるだけなら判別式 $D$ の符号から判断できます：
$D>0$ なら共有点の個数は2つ
$D=0$ なら共有点の個数は 1つ（グラフは $x$ 軸と接する）
$D<0$ なら共有点の個数は 0つ

例題２と同じ関数です。判別式 $D$ は
$D=5^2-4\cdot 2\cdot (-1)=33>0$
なので共有点の個数は2つだと分かります。
わざわざ二次方程式を解かなくても分かるので少し楽です。

判別式は
$D=1^2-4\cdot 1\cdot 1=-3<0$
なので共有点の個数は0（共有点を持たない）だと分かります。

次回は 相加平均、相乗平均の不等式の意味と使い方 を解説します。