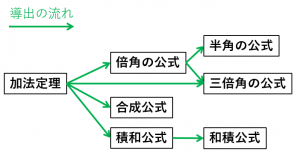
加法定理は、三角関数に関する重要な公式です。加法定理に関する公式22個を整理しました。下図の公式を全て理解すれば、三角関数は完璧です。
加法定理
$\sin$ の加法定理
1.$\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta$
2.$\sin(\alpha-\beta)=\sin\alpha\cos\beta-\cos\alpha\sin\beta$
$\cos$ の加法定理
3.$\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta$
4.$\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta$
$\tan$ の加法定理
5.$\tan(\alpha+\beta)=\dfrac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta}$
6.$\tan(\alpha-\beta)=\dfrac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta}$
重要度★★★:非常に重要です。
暗記必要度★★★:必ず覚えましょう。
倍角の公式
7.$\sin 2\alpha=2\sin\alpha\cos\alpha$
8.$\cos 2\alpha\\
=\cos^2\alpha-\sin^2\alpha\\
=2\cos^2\alpha-1\\
=1-2\sin^2\alpha$
9.$\tan\alpha=\dfrac{2\tan\alpha}{1-\tan^2\alpha}$
重要度★★☆:重要です。
暗記必要度★☆☆:暗記は不要です。加法定理から導出できるようになっておきましょう。
倍角の公式は、加法定理で $\alpha=\beta$ とすれば証明できます。詳細は、2倍角の公式の証明と頻出例題を確認してください。
半角の公式
10.$\sin^2\dfrac{\alpha}{2}=\dfrac{1-\cos\alpha}{2}$
11.$\cos^2\dfrac{\alpha}{2}=\dfrac{1+\cos\alpha}{2}$
12.$\tan^2\dfrac{\alpha}{2}=\dfrac{1-\cos\alpha}{1+\cos\alpha}$
重要度★★☆:重要です。
暗記必要度★★☆:倍角の公式から導出できますが、時間短縮のために暗記しておいてもよいでしょう。
半角の公式は、倍角の公式で $\alpha\to\dfrac{\alpha}{2}$ とすれば証明できます。詳細は半角の公式の使い方、導出、覚え方を確認してください。
三倍角の公式
13.$\sin 3\alpha=-4\sin^3\alpha+3\sin\alpha$
14.$\cos 3\alpha=4\cos^3\alpha-3\cos\alpha$
重要度★☆☆:使う機会は比較的少ないです。
暗記必要度★★☆:倍角の公式から導出できますが、時間短縮のために暗記しておいてもよいでしょう。
三倍角の公式は、加法定理で $\beta=2\alpha$ として、倍角の公式を使えば証明できます。
三角関数の合成
15.$a\sin\theta+b\cos\theta=\sqrt{a^2+b^2}\sin(\theta+\alpha)$
ただし、$\cos\alpha=\dfrac{a}{\sqrt{a^2+b^2}}$、$\sin\alpha=\dfrac{b}{\sqrt{a^2+b^2}}$
重要度★★☆:重要です。
暗記必要度★★★:加法定理から導出できますが、時間短縮のために暗記しておいた方がよいでしょう。
三角関数の積和公式
16.$\sin\alpha\cos\beta=\dfrac{1}{2}\{\sin(\alpha+\beta)+\sin(\alpha-\beta)\}$
17.$\cos\alpha\cos\beta=\dfrac{1}{2}\{\cos(\alpha+\beta)+\cos(\alpha-\beta)\}$
18.$\cos\alpha\cos\beta=-\dfrac{1}{2}\{\cos(\alpha+\beta)-\cos(\alpha-\beta)\}$
重要度★★☆:重要です。
暗記必要度★☆☆:暗記の必要性は低いです。加法定理から導出できるようになっておきましょう。
三角関数の和積公式
19.$\sin A+\sin B=2\sin\dfrac{A+B}{2}\cos\dfrac{A-B}{2}$
20.$\sin A-\sin B=2\cos\dfrac{A+B}{2}\sin\dfrac{A-B}{2}$
21.$\cos A+\cos B=2\cos\dfrac{A+B}{2}\cos\dfrac{A-B}{2}$
22.$\cos A-\cos B=-2\sin\dfrac{A+B}{2}\sin\dfrac{A-B}{2}$
重要度★☆☆:使う機会は比較的少ないです。
暗記必要度★★★:加法定理から導出できますが、時間短縮のために暗記しておいた方がよいでしょう。
次回は 三角方程式の解き方と例題 を解説します。
