三角方程式の解き方
手順1:$\sin ○=△$、$\cos ○=△$、$\tan ○=△$ のうちのどれかの形に変形する。
手順2:単位円を書いて角度を求める。
$\sin$ を含む三角方程式、$\cos$ を含む三角方程式、$\tan$ を含む三角方程式、それぞれについて解説します。
$\sin$ を含む方程式
例題1:$\sin\theta=\dfrac{1}{2}$ を、$0\leq\theta < 2\pi$ の範囲で解け。
すでに $\sin ○=△$ という形になっており、手順1は完了しています。
単位円と $y=\dfrac{1}{2}$ の交点に対応する角度が答えです。
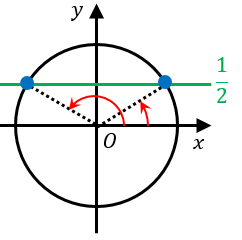
これを求めると、$\theta=\dfrac{\pi}{6}, \dfrac{5}{6}\pi$ です。
~補足~
単位円上の点の $y$ 座標が $\sin$ を表します。
関連:単位円を使った三角比の定義と有名角の値(0°~180°))
$\cos$ を含む方程式
例題2:$\cos\theta=-\dfrac{1}{2}$ を、$0\leq\theta < 2\pi$ の範囲で解け。
すでに $\cos ○=△$ という形になっており、手順1は完了しています。
単位円と $x=-\dfrac{1}{2}$ の交点に対応する角度が答えです。
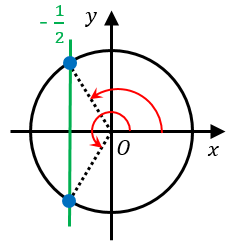
これを求めると、$\theta=\dfrac{2}{3}\pi,\dfrac{4}{3}\pi$ です。
$\tan$ を含む方程式
単位円上の点と原点を結ぶ直線の傾きが $\tan$ を表します。
例題3:$\tan\theta=\sqrt{3}$ を、$0\leq\theta < 2\pi$ の範囲で解け。
すでに $\tan ○=△$ という形になっており、手順1は完了しています。
原点を通り、傾き $\sqrt{3}$ の直線 $y=\sqrt{3}x$ と単位円との交点に対応する角度が答えです。
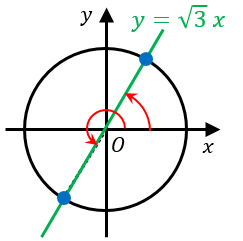
これを求めると、$\theta=\dfrac{1}{3}\pi,\dfrac{4}{3}\pi$ です。
二次の三角方程式
例題4:$-2\sin^2\theta-\cos\theta +1=0$ を $0\leq\theta < 2\pi$ の範囲で解け。
$\sin^2\theta+\cos^2\theta=1$ なので、
$\sin^2\theta=1-\cos^2\theta$ です。これを方程式に代入すると、
$-2(1-\cos^2\theta)-\cos\theta +1=0$
$2\cos^2\theta -\cos\theta -1=0$
となり、$\cos$ だけの式になります。これを因数分解すると、
$(2\cos\theta+1)(\cos\theta-1)=0$
となります。よって、
$\cos\theta=-\dfrac{1}{2},1$
となります。ここまでで手順1が完了です。
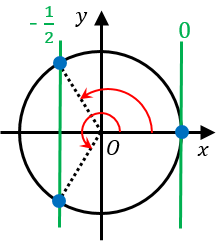
次に、単位円を書いて、$x=-\dfrac{1}{2}$、$x=1$ との交点に対応する角度を求めると、
$\theta=0,\dfrac{2}{3}\pi,\dfrac{4}{3}\pi$
となります。
次回は 2倍角の公式の証明と頻出例題 を解説します。
