一次関数について基本から分かりやすく解説

このページでは、一次関数について基本的な知識を解説します。傾き、切片、変化の割合、変域など、一次関数に関係する用語も説明します。

一次関数の例

・お風呂に水が３リットル溜まっています。
・さらに、水を１分あたり２リットルのペースで注ぎます。

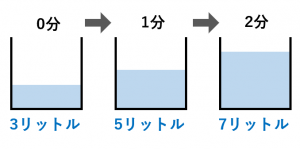
このとき、$x$ 分後にお風呂にたまっている水の量を $y$ リットル とすると、
$x=0$ のとき $y=3$
$x=1$ のとき $y=5$
$x=2$ のとき $y=7$
などとなります。つまり、
$y=2x+3$
という関係式が成り立ちます。

このように、２つの変数 $x,y$ の間に、
$y=ax+b$
という関係式が成立する時、この関係を一次関数と言います。

一次関数の傾きと切片

例えば、$y=2x+3$ という一次関数について
・傾きは $2$
・切片は $3$
です。

傾きと切片の意味は、傾きと切片の意味と求め方を丁寧に解説を参照してください。

一次関数のグラフ

例えば、$y=2x+3$ のグラフを書いてみましょう。

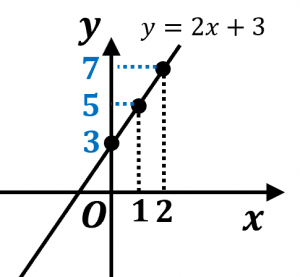
$x=0$ のとき $y=3$
$x=1$ のとき $y=5$
$x=2$ のとき $y=7$
などに注意してグラフを書くと、図のような直線になります。

一次関数のグラフは直線になることが分かっています。そのため、通る２点を計算して、それらを通る直線を書けばOKです。

一次関数の変域

例えば、先ほどのお風呂の例では、水を注ぐ時間 $x$ と水の量 $y$ の間には
$y=2x+3$
という関係がありました。

ここで、水を注ぐのを、５分後にやめたとします。このとき、
$x$ の変域は $0\leq x\leq 5$
です。また、$x=0$ のとき $y=3$ で、$x=5$ のとき $y=13$ なので、
$y$ の変域は $3\leq y\leq 13$
となります。

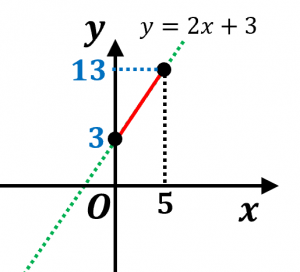
一次関数の変域を考えるときは、変域内では実線、変域外では点線のグラフを書くと分かりやすいです。

ちなみに、
$x$ の変域のことを「定義域」とも言います。
$y$ の変域のことを「値域」とも言います。

一次関数の変化の割合

つまり、
変化の割合＝$y$ の増加量 $\div$ $x$ の増加量
です。

例えば、$y=2x+3$ の場合、
$x$ が $0$ から $5$ に増えると、$y$ は $3$ から $13$ に増えます。つまり、$x$ の増加量は $5$ で $y$ の増加量は $10$ です。

よって、変化の割合は、$10\div 5=2$ となります。

変化の割合は、傾きである $2$ と一致しました。このように、一次関数 $y=ax+b$ では、変化の割合は必ず $a$ になります：
変化の割合＝傾き＝$a$

一次関数と比例

つまり「比例」は「一次関数の特殊な場合」です。

ちなみに、$a=0$ の場合は、$y=b$ となりますが、この関係式は正確には一次関数とは言わず、定数関数と言います。

一次関数の正確な定義

「関数」とは？
「$x$ の値が決まったら $y$ の値が１つに決まる」とき「$y$ は $x$ の関数である」と言います。

「一次の」とは？
次数が１であるような多項式のことです。次数とは、$x$ がかけられている回数（の最大値）です。例えば $x^2$ は次数が２次なので、$y=x^2$ という関数は一次関数ではありません。
参考：次数の意味（単項式、多項式、特定の文字に着目）

次回は 不等号＜、＞、≦、≧の読み方（日本語、英語） を解説します。