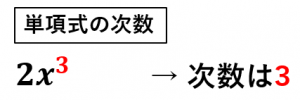
次数とは、大雑把に言うと、かけ合わされている文字の個数です。例えば、$2x^3$ という式は $x$ が3個かけ合わされているので、次数は3になります。
このページでは、
・次数の意味は?
・多項式の場合の次数は?
・特定の文字に着目したときの次数は?
といった、次数に関する疑問にお答えします。
単項式の次数と具体例
例えば、$2x^3$ の次数は $3$ です。$2\times x\times x\times x$ で文字が3つかけ合わされているとみなせるからです。
また、$3a^3b^2c$ の次数は $6$ です。$a$ が3個、$b$ が2個、$c$ が1個で合計6個の文字がかけ合わされているからです。
多項式の次数と具体例
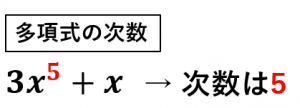
例えば、$3x^5+x$ の次数を求めてみましょう。
まず「それぞれの単項式の次数」を計算してみると、
・$3x^5$ の次数は5
・$x$ の次数は1
なので、5と1の中で最大のものを選ぶと次数は5になります。
また、$2x+3y^3+4xy$ の次数を求めてみましょう。
・$2x$ の次数は1
・$3y^3$ の次数は3
・$4xy$ の次数は2
なので、その中で最大のものを選ぶと次数は3になります。
特定の文字に着目した時の次数(単項式)
次に「特定の文字に着目したときの次数」の意味を説明します。
例えば、$2x^3y^2z$ について、$x$ に着目した時の次数を求めてみましょう。
かけられている $x$ の個数は $3$ つなので、$x$ に着目した時の次数は $3$ になります。
このように「$x$ に着目したときの次数」を考えるときは、$y$ や $z$ など、$x$ 以外の文字は数えません(無視します)。
複数の文字に着目したときの次数
例えば、$2x^3y^2z$ について、$x$ と $y$ に着目した時の次数は $5$ です。
$x$ が3個、$y$ が2個で合計5個です。このとき、$z$ は着目していないので無視します。
特定の文字に着目した時の次数(多項式)
・$x^3+y^5$ の次数は $5$ だが、$x$ に着目した時の次数は $3$
($x$ は3個かけ合わされている、$y$ は無視)
・$3a^2+ab^5+ac^3$ の次数は $6$ だが、$a$ に着目した時の次数は $2$
($b$ と $c$ は無視 $a$ が一番たくさんかけ合わされている項は $3a^2$ で、その個数は2個)
次回は 文字式のかけ算(乗法):やり方と例題5問 を解説します。