傾きと切片の意味と求め方を丁寧に解説

具体例で学ぶ数学 > 図形 > 傾きと切片の意味と求め方を丁寧に解説

最終更新日 2018/10/27

１次関数 $y=ax+b$ の $a$ を傾き、$b$ を切片と言います。

例えば、$y=2x-1$ の傾きは $2$、切片は $-1$ となります。

傾きと切片（数式から考える）

直線の式が分かっていれば、傾きと切片はすぐに求めることができます。

直線 $y=5x-4$ の傾きと切片を求めよ。

傾きは $x$ の係数 $5$
切片は定数項 $-4$
となります。

グラフを書いてみれば傾きと切片の意味がより深く理解できます。

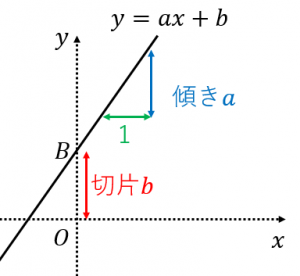
傾き
＝変化の割合
＝($y$ の増加量)÷($x$ の増加量)
＝$x$ が $1$ 増えたときの $y$ の増分

切片
＝ $x$ が $0$ のときの $y$ の値
＝点 $B$ から原点 $O$ までの距離
（$B$ が $O$ より下にあるときは距離を $-1$ 倍する必要があるので注意）

傾き $a$ が正
$\iff$ $x$ が増えると $y$ も増える
$\iff$ 直線は左下から右上に伸びる

傾き $a$ が負
$\iff$ $x$ が増えると $y$ は減る
$\iff$ 直線は左上から右下に伸びる

切片 $b$ が正 $\iff$ 直線は $y$ 軸と原点より上側で交わる
切片 $b$ が負 $\iff$ 直線は $y$ 軸と原点より下側で交わる

通る２点が与えられたときに、傾きと切片を求める方法について考えます。

$(1,3)$ と $(4,9)$ を通る直線の傾きと切片を求めよ。

まず、傾き＝($y$ の増加量)÷ ($x$ の増加量)を用いて傾き $a$ を求めます：
$a=\dfrac{9-3}{4-1}=\dfrac{6}{3}$$=2$

直線の方程式は $y=2x+b$ という形で表せることが分かりました。これに通る一点（どちらでもよい）を代入して切片 $b$ を求めます。$(1,3)$ を代入すると、
$3=2\cdot 1+b$
より $b=1$ です。

一般に、２点 $(x_1,y_1)$ と $(x_2,y_2)$ を通る直線の傾きは、$\dfrac{y_2-y_1}{x_2-x_1}$ と表すことができます。