二次関数の最大値と最小値は以下の3ステップで求める。
ステップ1:平方完成する
ステップ2:グラフを書く
ステップ3:最大値と最小値を求める
いろいろなパターンがありますが、必ず上の3ステップで解くことができます。
範囲なし、最大値がない問題
例題1:二次関数 $y=x^2+4x+1$ の最大値と最小値を求めよ。
ステップ1:平方完成します。
$y=x^2+4x+1$
$y=x^2+4x+4-4+1$
$y=(x+2)^2-3$
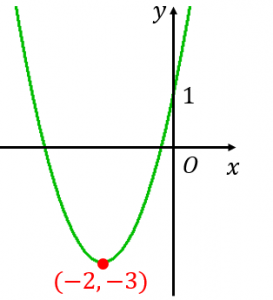
ステップ2:平方完成した式より、頂点の座標は $(-2,-3)$、軸は $x=-2$ であることが分かります。よって、グラフは図のようになります。
ステップ3:グラフより、答えは
最小値は $x=-2$ のとき $y=-3$
最大値は存在しない($x$ が増える、または減ると $y$ はどこまでも大きくなる)
なお、例題1と例題2の平方完成が分からない方は平方完成のやり方と練習問題を詳しく解説を参照してください。
範囲なし、最小値がない問題
例題2:二次関数 $y=-2x^2+12x-3$ の最大値と最小値を求めよ。
ステップ1:平方完成します。
$y=-2(x^2-6x)-3$
$y=-2(x^2-6x+9-9)-3$
$y=-2(x-3)^2+15$
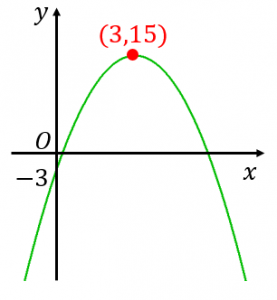
ステップ2:平方完成した式より、頂点の座標は $(3,15)$、軸は $x=3$ であることが分かります。よって、グラフは図のようになります。
ステップ3:グラフより、答えは
最小値は存在しない($x$ が増える、または減ると $y$ はどこまでも小さくなる)
最大値は $x=3$ のとき $y=15$
範囲ありの問題
例題3:二次関数 $y=x^2+4x+1$ の、$-3\leq x\leq 0$ における最大値と最小値を求めよ。
ステップ1:平方完成は例題1と同じです。
$y=(x+2)^2-3$
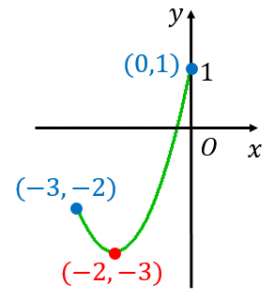
ステップ2:頂点、軸、グラフの形も例題1と同じですが、範囲が $-3\leq x\leq 0$ に制限されています。
ステップ3:グラフの両端は $(-3,-2)$、$(0,1)$ であることに注意すると
最小値は $x=-2$ のとき $y=-3$
最大値は $x=0$ のとき $y=1$
例題4:二次関数 $y=-2x^2+12x-3$ の、$0< x\leq 4$ における最大値と最小値を求めよ。
ステップ1:平方完成は例題1と同じです。
$y=-2(x-3)^2+15$
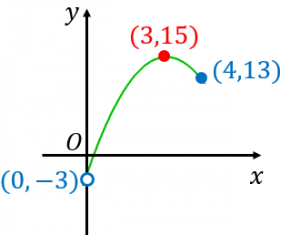
ステップ2:頂点、軸、グラフの形も例題2と同じですが、範囲が $0< x\leq 4$ に制限されています。
ステップ3:両端は $(0,-3)$、$(4,13)$ です。ただし、$(0,-3)$ はギリギリ範囲の外です。よって、
最小値は存在しない
最大値は $x=3$ のとき $y=15$
次回は 二次関数のグラフとx軸の共有点の座標を求める を解説します。
